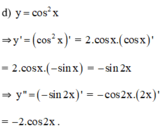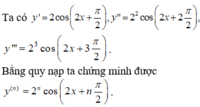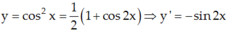tính đạo hàm cấp hai của hàm số y= x(1+sin2x) + 1/2 cos2x

Những câu hỏi liên quan
Tính đạo hàm của hàm số sau
y
sin
2
x
+
cos
2
x
2
sin
2
x
−
cos
2
x
.
A.
6
2
sin...
Đọc tiếp
Tính đạo hàm của hàm số sau y = sin 2 x + cos 2 x 2 sin 2 x − cos 2 x .
A. 6 2 sin 2 x − cos 2 x 2
B. − 6 sin 2 x − cos 2 x 2
C. 6 2 sin 2 x − cos x 2
D. − 6 2 sin 2 x − cos 2 x 2
Chọn D
y ' = sin 2 x + cos 2 x / . 2 sin 2 x − cos 2 x − 2 sin 2 x − cos 2 x / . sin 2 x + cos 2 x 2 sin 2 x − cos 2 x 2
y ' = 2 cos 2 x − 2 sin 2 x 2 sin 2 x − cos 2 x − 4 cos 2 x + 2 sin 2 x sin 2 x + cos 2 x 2 sin 2 x − cos 2 x 2 = 4. c os2x. sin2x - 2cos 2 2 x − 4 sin 2 2 x + 2. sin 2 x . c os2x ( 2 sin 2 x − cos 2 x ) 2 − ( 4cos2x . sin2x + 4cos 2 2 x + 2 sin 2 2 x + 2 sin 2 x . c os2x ( 2 sin 2 x − c os2x) 2
y ' = − 6 cos 2 2 x − 6 sin 2 2 x 2 sin 2 x − cos 2 x 2 = − 6 2 sin 2 x − cos 2 x 2
Đúng 0
Bình luận (0)
Tính đạo hàm cấp hai của các hàm số sau: y = cos 2 x
Tính đạo hàm cấp hai của hàm số sau y sin5x. cos2x A.
y
1
2
-
49
sin
7
x
+
9
sin
3
x
B.
y...
Đọc tiếp
Tính đạo hàm cấp hai của hàm số sau y = sin5x. cos2x
A. y ' ' = 1 2 - 49 sin 7 x + 9 sin 3 x
B. y ' ' = - 1 2 49 sin 7 x + 9 sin 3 x
C. y ' ' = 1 2 49 sin 7 x - 9 sin 3 x
D. Đáp án khác
y ' = 2 2 − 3 x 2 x + 1 . 2 − 3 x 2 x + 1 ' = 2 2 − 3 x 2 x + 1 . − 3 2 x + 1 − 2 2 − 3 x 2 x + 1 2 = 2 2 − 3 x 2 x + 1 . − 7 2 x + 1 2 = − 14 2 x + 1 2 . 2 − 3 x 2 x + 1
Chọn đáp án A
Đúng 0
Bình luận (0)
Tìm đạo hàm của hàm số sau: y = sin ( cos 2 x ) . cos ( sin 2 x )
Tính đạo hàm cấp n của hàm số y cos2x A. B. C. D.
Đọc tiếp
Tính đạo hàm cấp n của hàm số y = cos2x
A. 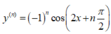
B. 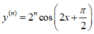
C. 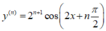
D. 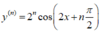
Đạo hàm của hàm số y cos6x + sin4x. cos2x + sin2x. cos4x + sin4x – sin2x bằng biểu thức nào sau đây? A.
-
6
cos
5
x
sin
x
B.
6
cos
5
x
sin
x
C.
6
sin
5
x
cos
x
D.
6
cos
5...
Đọc tiếp
Đạo hàm của hàm số y = cos6x + sin4x. cos2x + sin2x. cos4x + sin4x – sin2x bằng biểu thức nào sau đây?
A. - 6 cos 5 x sin x
B. 6 cos 5 x sin x
C. 6 sin 5 x cos x
D. 6 cos 5 x
Chọn A
y = cos6 x+ sin2xcos2x(sin2x + cos2x) + sin4x - sin2x
= cos6x + sin2x(1 - sin2x) + sin4x - sin2x = cos6x
Do đó : y' = -6cos5xsinx.
Đúng 0
Bình luận (0)
Tính đạo hàm đến cấp đã chỉ ra của hàm số sau: y = cos2x,(y’’’)
A: sin2x
B: 2 sin2x
C: sin 4x
D: 4sin2x
Đạo hàm cấp hai của hàm số y= cos2x bằng biểu thức nào sau đây?
A. -2sin2x
B. -4cos2x
C. -4sin2x
D. 4cos2x
Tính đạo hàm đến cấp đã chỉ ra của hàm số sau: y = x4 – sin2x, (y(4))
A: 16 - 8sin 2x
B: 24 - 8sin2x
C: 24 - 16sin2x
D: 16 - 24sin2x
Chọn C.
y = x4 - sin2x
⇒ y’ = 4x3 – 2cos2x ⇒ y’’ = 12x2 + 4sin2x
⇒ y’’’ = 24x + 8cos2x ⇒ y(4) = 24 – 16sin2x
Đúng 0
Bình luận (0)