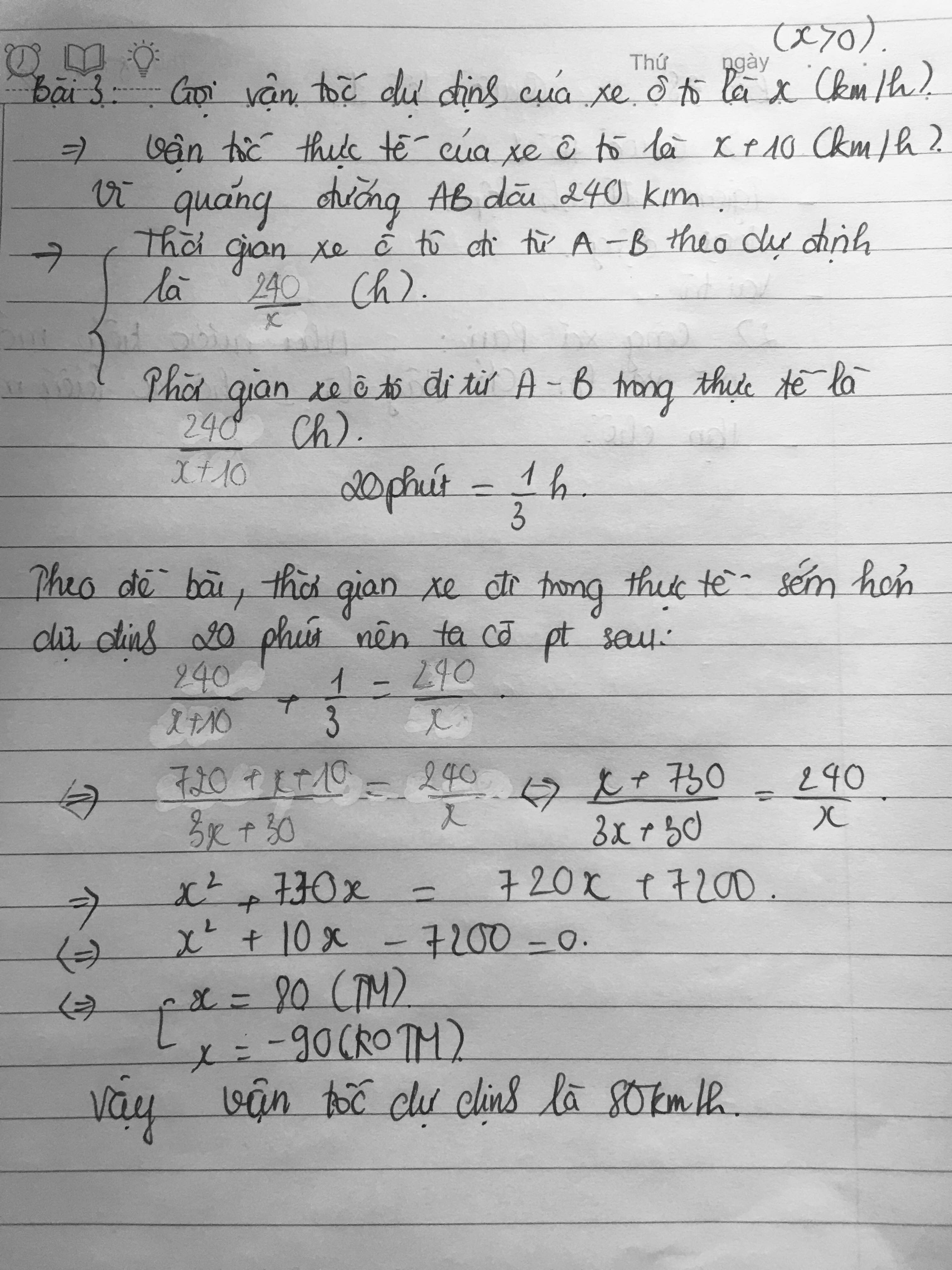Giải giúp 5 bài

Những câu hỏi liên quan
 Giải bài 4 và bài 5 và bài 6 nhớ giải chi tiết giúp mik
Giải bài 4 và bài 5 và bài 6 nhớ giải chi tiết giúp mik
Giải giúp mình bài Bài 4 Bài 5 với ạ
Đọc tiếp


Giải giúp mình bài Bài 4 Bài 5 với ạ
 giải giúp mik đề 4
giải giúp mik đề 4
Bài 3, Bài 4, Bài 5, Bài 6
Giải giúp mình bài 4 bài 5 với ạ!
Đọc tiếp


Giải giúp mình bài 4 bài 5 với ạ!
Giải giúp bài 5
ĐKXĐ: \(x\ge2\)
\(B=\sqrt{x-2-2\sqrt{x-2}+1}+\sqrt{x-2-6\sqrt{x-2}+9}\)
\(=\sqrt{\left(\sqrt{x-2}-1\right)^2}+\sqrt{\left(3-\sqrt{x-2}\right)^2}\)
\(=\left|\sqrt{x-2}-1\right|+\left|3-\sqrt{x-2}\right|\)
\(\ge\left|\sqrt{x-2}-1+3-\sqrt{x-2}\right|=2\)
Vậy \(B_{min}=2\), dấu "=" xảy ra khi \(1\le\sqrt{x-2}\le3\Rightarrow3\le x\le11\)
Đúng 2
Bình luận (1)
Bạn nào có sách bài tập toán lớp 5 tập 2 thì giải giúp mình bài 5 trang 19 và bài 3 trang 37 (nhớ giải chi tiết nha!)
bạn chép đề bài ra đi chứ mình cũng không biết
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
 Giải giúp bài 5 6 7 8 của bài 15 i
Giải giúp bài 5 6 7 8 của bài 15 i
`5)(6-sqrt6)/(1-sqrt6)+(6-sqrt6)/sqrt6=(sqrt6(sqrt6-1))/(1-sqrt6)+(sqrt6(sqrt6-1))/sqrt6=-sqrt6+sqrt6-1=-1` $\\$ `6)1/(sqrt2-sqrt3)-1/(sqrt3+sqrt2)=(sqrt2+sqrt3)/(2-3)-(sqrt3-sqrt2)/(3-2)=-(sqrt2+sqrt3)-sqrt3+sqrt2=-2sqrt3` $\\$ `7)1/(sqrt5+sqrt3)-1/(sqrt5-sqrt3)=(sqrt5-sqrt3)/(5-3)-(sqrt5+sqrt3)/(5-3)=(sqrt5-sqrt3-sqrt5-sqrt3)/2=-sqrt3` $\\$ `8)6/(1-sqrt3)-(3sqrt3-3)/(sqrt3+1)=(6(1+sqrt3))/(1-3)-(3(sqrt3-1)^2)/(3-1)=(-6(sqrt3+1)-3(4-2sqrt3))/2=-9`
Đúng 2
Bình luận (0)
16) Ta có: \(\dfrac{\sqrt{2}-\sqrt{3}}{2-\sqrt{6}}+\dfrac{\sqrt{3}-\sqrt{2}}{\sqrt{6}+2}\)
\(=\dfrac{\sqrt{2}-\sqrt{3}}{\sqrt{2}\left(\sqrt{2}-\sqrt{3}\right)}+\dfrac{\sqrt{3}-\sqrt{2}}{\sqrt{6}+2}\)
\(=\dfrac{1}{\sqrt{2}}+\dfrac{\sqrt{3}-\sqrt{2}}{\sqrt{2}\left(\sqrt{3}+\sqrt{2}\right)}\)
\(=\dfrac{\sqrt{3}+\sqrt{2}+\sqrt{3}-\sqrt{2}}{\sqrt{2}\left(\sqrt{3}+\sqrt{2}\right)}\)
\(=\dfrac{2\sqrt{3}}{\sqrt{2}\left(\sqrt{3}+\sqrt{2}\right)}\)
\(=\dfrac{\sqrt{6}}{\sqrt{3}+\sqrt{2}}\)
\(=\sqrt{18}-\sqrt{12}\)
\(=3\sqrt{2}-2\sqrt{3}\)
Đúng 0
Bình luận (0)
Giải bài 5 giúp mình
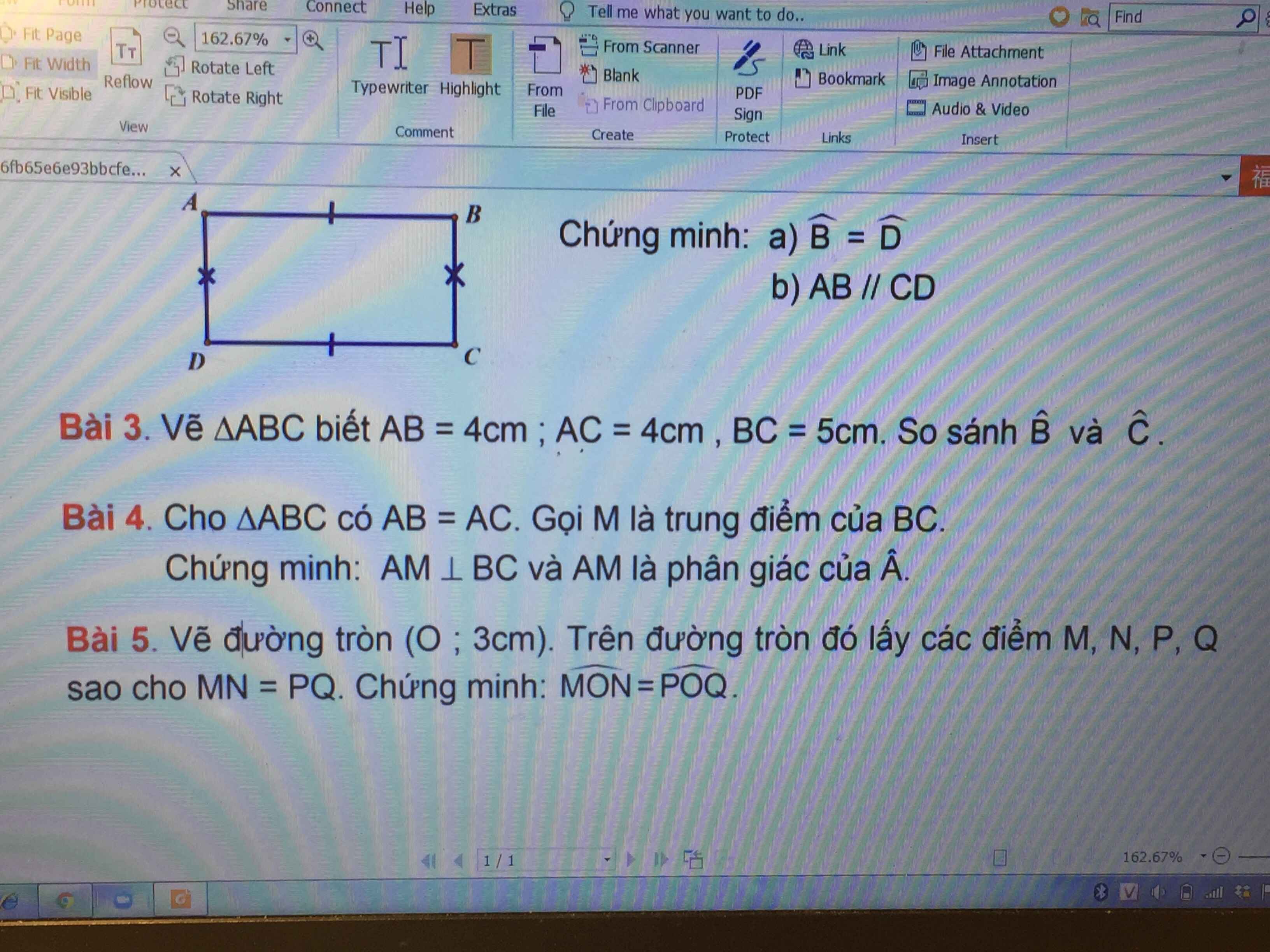
Mọi người giải giúp mình bài 5
Bài 5:
a: Vì 3046<4036<4603<6304<10000
và \(10000\le\overline{abcde}\)
nên viết theo thứ tự tăng dần thì ta sẽ có: 3046; 4036; 4603; 6304; \(\overline{abcde}\)
b: Ta có: 10000>6714>6517>6471>6174
và \(\overline{x2345}>10000\)
nên \(\overline{x2345}>6714>6517>6471>6174\)
=>Viết theo thứ tự giảm dần thì ta sẽ có:\(\overline{x2345};6714;6517;6471;6174\)
Đúng 0
Bình luận (0)