Giải bất phương trình 5x + 10 ≥ 0 và biểu diễn tập nghiệm trên trục số.

Những câu hỏi liên quan
Giúp e vs ạ Giải bất phương trình, biểu diễn tập nghiệm trên trục số: a) 5x + 15 > 0 b) -4x + 1 > 17 c) -5x + 10 < 0 d)
Em tự biểu diễn nha.
\(a,5x+15>0\\ \Leftrightarrow5x>-15\\ \Leftrightarrow x>-3\)
\(b,-4x+1>17\\ \Leftrightarrow-4x>16\\ \Leftrightarrow x< -4\)
\(c,-5x+10< 0\\ \Leftrightarrow-5x< -10\Leftrightarrow x>2\)
Đúng 4
Bình luận (0)
giải bất phương trình và biểu diễn tập nghiệm trên trục số: 5x+3<_ 2x+9
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số: a, 5x+10<=0. b,2x+4>3x+3. C, 2x+4=>2(x+1)-3. d, 2(x+1)<5(x-2)-3x.
c: =>2x+4>=2x+2-3
=>4>=-1(luôn đúng)
a: 5x+10>3x+3
=>2x>-7
=>x>-7/2
Đúng 1
Bình luận (0)
a: =>x+2<=0
=>x<=-2
b: =>-x>-1
=>x<1
c: =>2x+4>=2x+2-3
=>4>=-1(luôn đúng)
d: =>2x+2<5x-10-3x
=>2x+2<2x-10
=>2<-10(loại)
Đúng 1
Bình luận (0)
Giải bất phương trình và biểu diễn tập nghiệm trên trục số: 2x - 3 > 0
2x – 3 > 0
⇔ 2x > 3 (Chuyển vế -3).
⇔ 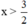 (Chia cả hai vế cho 2 > 0, BĐT không đổi chiều).
(Chia cả hai vế cho 2 > 0, BĐT không đổi chiều).
Vậy BPT có nghiệm 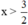

Đúng 0
Bình luận (0)
Giải bất phương trình - 4x – 8 < 0 và biểu diễn tập nghiệm trên trục số.
-4x – 8 < 0 ⇔ -4x < 8
⇔ -4x : (- 4) > 8: (- 4) ⇔ x > -2
Vậy tập nghiệm của bất phương trình -4x – 8 < 0 là {x|x > -2}
Biểu diễn trên trục số
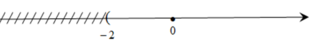
Đúng 0
Bình luận (0)
Giải bất phương trình và biểu diễn tập nghiệm trên trục số: 3x + 4 < 0
3x + 4 < 0
⇔ 3x < -4 (chuyển vế 4).
⇔ 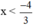 (Chia cả hai vế cho 3 > 0).
(Chia cả hai vế cho 3 > 0).
Vậy BPT có tập nghiệm 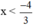

Đúng 1
Bình luận (0)
Giải bất phương trình và biểu diễn tập nghiệm trên trục số: 4 - 3x ≤ 0
4 – 3x ≤ 0
⇔ -3x ≤ -4 (Chuyển vế hạng tử 4).
⇔ 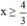 (Chia cả hai vế cho -3 < 0, BPT đổi chiều).
(Chia cả hai vế cho -3 < 0, BPT đổi chiều).
Vậy BPT có tập nghiệm 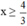

Đúng 0
Bình luận (0)
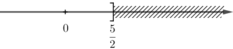
Giải bất phương trình và biểu diễn tập nghiệm trên trục số: 5 - 2x ≥ 0
5 – 2x ≥ 0
⇔ -2x ≥ -5 (Chuyển vế hạng tử 5).
⇔ 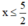 (Chia cả hai vế cho -2 < 0, BĐT đổi chiều).
(Chia cả hai vế cho -2 < 0, BĐT đổi chiều).
Vậy BPT có nghiệm 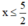
Đúng 0
Bình luận (0)
Câu 1 Giải bất phương trình sau, biểu diễn tập nghiệm trên trục số
2x+4 > 5x -11
Câu 2 Giải phương trình
|x+10|=5x-2
2x + 4 > 5x - 11
<=> 2x - 5x > -11 - 4
<=> -3x > -15
<=> -3x : ( -3 ) < -15 : ( -3 )
<=> x < 5
Vậy tập nghiệm của bất phương trình là x < 5
Giải bất phương trình và biểu diễn tập nghiệm trên trục số a)x-20c)-5x+3>_2x (Giải giúp em vs ạ)
















