cho ΔABC ⊥ tại A, góc B bằng 30 độ. vẽ CD=AC, DE⊥AB:
a) Chứng minh AD=BD
Những câu hỏi liên quan
Cho ΔABC cân tại A (Å < 90 độ). Vẽ BE vuông góc với AC tại E, CD vuông góc với AB tại D.
a/ Chứng minh BE = CD
b/ Cho BC = 10cm, BD = 6cm. Tính CD
c/ Chứng minh AD = AE
d/ Gọi I là giao điểm của BE và CD. Chứng minh ΔBIC cân
e/ Chứng minh AI là tia phân giáp của góc BAC
a: Xét ΔABE vuông tại E và ΔACD vuông tại D có
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACD
b: \(CD=\sqrt{10^2-6^2}=8\left(cm\right)\)
c: Ta có: ΔABE=ΔACD
nên AE=AD
d: Xét ΔDBC vuông tại D và ΔECB vuông tại E có
BC chung
DC=BE
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{IBC}=\widehat{ICB}\)
hay ΔBIC cân tại I
Đúng 0
Bình luận (0)
Cho ΔABC cân tại A. Vẽ phân giác BD,CE.
a) Chứng minh: BD=CE
b) Chứng minh DE=BC
c) Biết AB=AC=6cm, BC=4cm. Tính AD, DC
Cho tam giác ABC cân tại A có góc B = góc C bằng 40 độ. Kẻ phân giác BD ( D thuộc AC). Trên tia AB lấy điểm M sao cho AM = BC. Từ D dựng đường thẳng song song với BC cắt AB tại E.
a) Chứng minh DE = CD
b) Chứng minh BD + AD = BC
c) tính góc AMC
cho ΔABC vuông tại A (AB<AC), kẻ đường cao AD
1) chứng minh ΔBAD đồng dạng với Δ BCA từ đó suy ra AB2 =BD*BC
2)cho BD bằng 2cm, BC bằng 32 cm. tính AD
3)cho góc ACB =30 độ, tia phân giác góc ABC cắt AD tại F và cắt AC tại E. tính AB2= AE*AC
1. xét tam giác BAD và tam giác BCA:
góc D= góc A = 90o
góc B chung
=> tam giác BAD ~ tam giác BCA (g.g)
=> \(\dfrac{AB}{BC}\)=\(\dfrac{BD}{AB}\)
=> AB2=BD.BC
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A (AB < AC), BD là phân giác của góc B. Gọi E là hình
chiếu của D trên BC
a) Biết AB = 9cm; AC = 12cm. Tính BC.
b) Chứng minh ΔDAE cân.
c) Chứng minh DA < DC.
d) Vẽ CF vuông góc với BD tại F. Chứng minh các đường thẳng AB, DE, CF đồng quy
a, Xét ΔABC có AB=9cm, AC=12cm, ∠A=90độ
Áp dụng định lý Py-ta-go:
BC²=AB²+AC²
→BC²=9²+12²
→BC²=225
→BC=15CM
b, Xét ΔABD và ΔEBD có:
∠ABD=∠EBD (BD là tia phân giác)
BD-chung
∠BAD=∠BED=90 độ
→ΔABD=ΔEBD (g.c.g)
→AD=ED (cặp góc tương ứng)
→ΔDEA cân
c, Xét ΔDEC có ∠DEC= 90 độ và DC là cạnh huyền
mà trong tam giác vuông cạnh huyền là cạnh lớn nhất
nên DC>DE
mà DE=DA
suy ra DC>DA
d, Gọi K là giao điểm của AB và CF
Xét ΔBCK có: BF và CA là hai đường cao
và BF∩CA≡D
Mà DE⊥BC→DE∈đường cao từ K
→K,D,E thẳng hàng
→ AB,BE,CF đồng quy
Đúng 0
Bình luận (0)
Cho ΔABC cân tại A ( góc A < 90 độ ) . Kẻ BD ⊥ AC tại D , kẻ CE ⊥ AB tại E
a, Chứng minh ΔADE CÂN
b, DE // BC
c, Gọi I là giao diểm của BD và CE . Chứng minh IB = IC
d, AI ⊥ BC
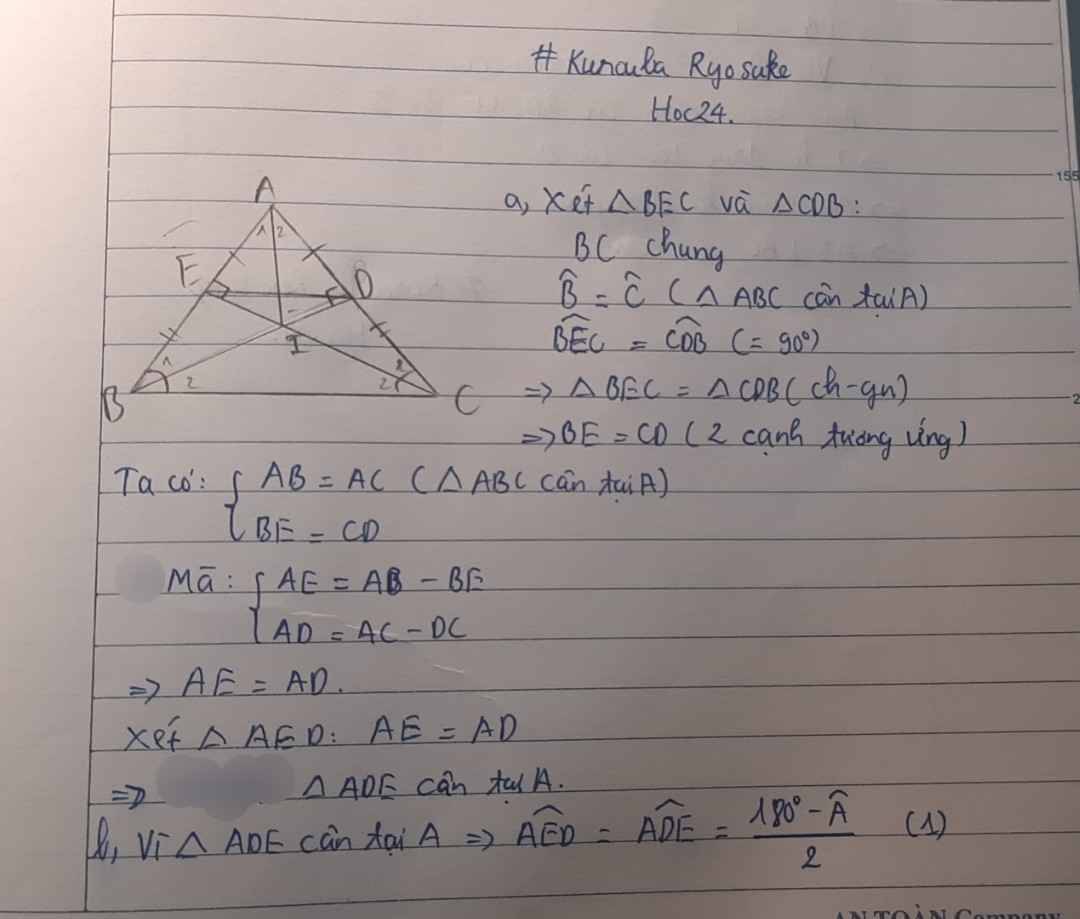
* câu d, í cậu, nếu cậu chưa học về các đường và t/c của tam giác cân với các đường đó thì bảo mk để mk làm lại cách khác cho nha :vv.
Đúng 3
Bình luận (2)
1. Cho ΔABC. Trên nửa mặt phẳng bờ AB không chứa điểm B vẽ AD ⊥ và bằng AB; Trên nửa mặt phẳng bờ AC không chứa điểm C vẽ AE ⊥ và bằng AC.a) Chứng minh CD BE và CD ⊥ BEb) Gọi M là trung điểm của BC. Chứng minh AM 1/2 DE và AM ⊥ DE2. Cho ΔABC qua A vẽ một đường thẳng xy // BC. Từ điểm M trên cạnh BC vẽ các đường thẳng // AB và AC chúng cắt xy theo thứ tự tại D và E. Cmr:a) ΔABC ΔMDEb) Ba đường thẳng AM, DB, CE cùng đi qua một điểm( đồng qui)3. ΔABC vuông cân tại A, có cạnh AB 1cm. Vẽ AH ⊥ BC...
Đọc tiếp
1. Cho ΔABC. Trên nửa mặt phẳng bờ AB không chứa điểm B vẽ AD ⊥ và bằng AB; Trên nửa mặt phẳng bờ AC không chứa điểm C vẽ AE ⊥ và bằng AC.
a) Chứng minh CD = BE và CD ⊥ BE
b) Gọi M là trung điểm của BC. Chứng minh AM = 1/2 DE và AM ⊥ DE
2. Cho ΔABC qua A vẽ một đường thẳng xy // BC. Từ điểm M trên cạnh BC vẽ các đường thẳng // AB và AC chúng cắt xy theo thứ tự tại D và E. Cmr:
a) ΔABC = ΔMDE
b) Ba đường thẳng AM, DB, CE cùng đi qua một điểm( đồng qui)
3. ΔABC vuông cân tại A, có cạnh AB = 1cm. Vẽ AH ⊥ BC (H ∈ BC).
a) Chứng minh ΔABH = ΔACH
b) Tính AH
c) M là một điểm di chuyển trên cạnh BC, kẻ MP, MQ lần lượt ⊥ AB và AC. Chứng minh MP + MQ không đổi.
cho tam giác ABC có C = 30 độ . Vẽ đường phân giác AD(D thuộc BC) . Vẽ DE vuông góc với AB , DF vuông góc với AC . Chứng minh : a,tam giác DEF đều .b, tam giác BED = tam giác CFD c, từ B vẽ đường thẳng song song với AD cắt AC tại M . chứng minh tam giác ABM đều . d, tính độ dài đoạn BD . nếu AD =4cm
Cho ΔABC , góc A =90 độ , góc B=60độ .
a, So sánh AD và BD
b, Trên BC lấy D sao cho BD=AB . Qua D dựng đường vuông góc với BC cắt tia đối của AB tại E . Chứng minh : ΔABC=ΔDBE
c, H là giao điểm của AC và ED . Chứng minh : BH là phân giác của góc ABC
d, Qua B vẽ đường thẳng vuông góc AB cắt ED tại K . Chứng minh : ΔHBK đều
b) Xét ΔABC vuông tại A và ΔDBE vuông tại D có
AB=BD(gt)
\(\widehat{ABC}\) chung
Do đó: ΔABC=ΔDBE(cạnh góc vuông-góc nhọn kề)
c) Xét ΔBAH vuông tại A và ΔBDH vuông tại D có
BH chung
BA=BD(gt)
Do đó: ΔBAH=ΔBDH(Cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{ABH}=\widehat{DBH}\)(hai góc tương ứng)
hay BH là tia phân giác của \(\widehat{ABC}\)
d) Ta có: BH là tia phân giác của \(\widehat{ABC}\)(cmt)
nên \(\widehat{ABH}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)
Ta có: \(\widehat{ABH}+\widehat{HBK}=90^0\)
\(\Leftrightarrow\widehat{HBK}+30^0=90^0\)
hay \(\widehat{HBK}=60^0\)
Xét ΔCHD vuông tại D và ΔCBA vuông tại A có
\(\widehat{ACB}\) chung
Do đó: ΔCHD\(\sim\)ΔCBA(g-g)
Suy ra: \(\widehat{CHD}=\widehat{CBA}\)(hai góc tương ứng)
\(\Leftrightarrow\widehat{CHD}=60^0\)
mà \(\widehat{CHD}=\widehat{HKB}\)(hai góc so le trong, BK//AC)
nên \(\widehat{HKB}=60^0\)
Xét ΔHBK có
\(\widehat{HKB}=60^0\)(cmt)
\(\widehat{HBK}=60^0\)(cmt)
Do đó: ΔHBK đều(Dấu hiệu nhận biết tam giác đều)
Đúng 0
Bình luận (1)