cho tam giác ABC, ba đường cao AD,BE,CF.biết AD=BD=CF. chứng minh tam giác ABC là tam giác đều

Những câu hỏi liên quan
Cho tam giác nhọn ABC có ba đường cao AB, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.
Tham khảo:
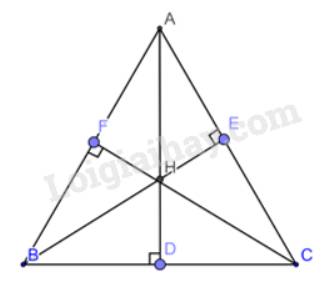
Xét tam giác BFC và tam giác BEC có :
BC chung
FC = BE
\(\widehat {BFC} = \widehat {BEC} = {90^o}\)
( cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat B\) ( 2 góc tương ứng ) (1)
Xét tam giác CFA và tam giác ADC ta có :
CF = AD
AC chung
\(\widehat {ADC} = \widehat {AFC} = {90^o}\)
(cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat A\)(2 góc tương ứng ) (2)
Từ (1) và (2) \( \Rightarrow \widehat C = \widehat A = \widehat B\) \( \Rightarrow \)Tam giác ABC là tam giác đều do có 3 góc bằng nhau
Đúng 0
Bình luận (0)
cho tam giác abc, 3 đường cao AD, BE,CF. Biết AD=BE=CF. chứng minh tam giác ABC đều
cho tam giác abc đều, ad, be, cf là đường trung tuyến. chứng minh ad, be, cf là đường cao và đường phân giác. gấp ạ
Ta có: ΔABC đều
mà AD,BE,CF là các đường trung tuyến
nên AD,BE,CF vừa là đường cao vừa là phân giác
Đúng 0
Bình luận (0)
a) Cho tam giác ABC, vẽ đường thẳng đi qua A cắt cạnh BC tại K và cắt trung tuyến BM tại I sao cho BI : IM = 1:2 Tính tỉ số diện tích của tam giác ABK và diện tích tam giác ABC
b) Cho tam giác ABC có ba đường cao AD, BE và CF thỏa mãn AD + BC = BE + AC = CF + AB
Chứng minh tam giác ABC là tam giác đều
Bài 8. Cho tam giác ABC. Dựng ngoài tam giác đó các tam giác đều BCD, ACE, ABF. Chứng minh rằng:
a) Ba đường tròn ngoại tiếp tam giác đều nói trên đều đi qua 1 điểm
b) Ba đường thẳng AD, BE,CF bằng nhau
c) Ba đoạn thẳng AD,BE,CF bằng nhau
Tam giác abc có ba góc nhọn đường cao AD,BE, CF cắt nhau ở H
a, chứng minh BD nhân BC = BE nhân BA
b, tam giác BDF đồng dạng với tam giác BAC
c, góc CDE bằng góc BAC
d, DH là đường phân giác góc FDE
a) cho ABC ,vẽ đường thẳng đi qua A cắt BC tại K và cắt trung tuyến BM tại I sao cho BI:IM= 1:2 Tính ti số diện tích của tam giác ABK và điện tích tam giác ABC b) Cho tam giác ABC có 3 đường cao AD,BE,CF thỏa mãn AD+BC=BE+AC=CF+AB Chứng minh tam giác ABC là tam giác đều
Cho tam giác ABC nhọn có ba đường cao AD, BE, CF với H là trực tâm. Chứng minh tam giác AHE đồng dạng tam giác BHD; Chứng minh HA . HD = HB . HE
Xét ∆AHE và ∆BHD, ta có
<D=<E=90°
<BHD=<EHA ( đối đỉnh)
⟹ ∆AHE ∼∆BHD(g.g)
⟹HA/HB=HE/HD⟹ HA*HD=HB*HE
Đúng 0
Bình luận (0)
cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H. Biết:
diện tích tam giác ABC=diện tích tam giác BFD=diện tích tam giác CDE. Chứng minh: tam giác ABC đều
















