a ) Ta có : xOy + yOx ' = 180 ( kề bù )

          \(\Rightarrow\)  90 + yOx ' = 180

          \(\Rightarrow\)  yOx ' = 180 - 90 = 90

    Lại có : xOy + y ' Ox = 180 ( kề bù )

          \(\Rightarrow\)   90 + y ' Ox = 180

          \(\Rightarrow\)   y ' Ox = 180 - 90 = 90

    Ta thấy : xOy ' + y ' Ox ' = 180 ( kề bù )

          \(\Rightarrow\) 90 + y ' Ox ' = 180

          \(\Rightarrow\) y ' Ox ' = 180 - 90 = 90

b ) Ta có : xOy + yOx ' = 180 ( kề bù )

          \(\Rightarrow\)  30 + yOx ' = 180

          \(\Rightarrow\)  yOx ' =  180 - 30 = 150

   Lại có : xOy + yOx '= 180 ( kề bù )

          \(\Rightarrow\)  30 + yOx ' = 180

          \(\Rightarrow\)  yOx ' = 180 - 30 = 150

   Ta thấy : x ' Oy + y ' Ox ' = 180 ( kề bù )

          \(\Rightarrow\)   150 + y ' Ox ' = 180

          ⇒          y ' Ox ' = 180 - 150 = 3

Bài làm lại :

a ) \(\widehat{xOy}+\widehat{y'Oy}=180^o\)( KB )

\(\widehat{x'Oy}=180^o-\widehat{xOy}=180^o-90^o=90^o\)( Đối đỉnh )

Vậy \(\widehat{xOy}'=\widehat{y'Ox}=90^o\)( Đối đỉnh )

b ) \(\widehat{xOy}+\widehat{x'Oy}=180^o\)( KB )

\(\widehat{x'Oy}=180^o-\widehat{xOy}=180^o-30^o=150^o\)

Vậy \(\widehat{xOy}=\widehat{x'Oy'}=30^o\)( Đối đỉnh )

\(\widehat{yOx'}=\widehat{y'Ox}=150^o\)( Đối đỉnh )

Bài giải 

a) yOx' ; x'Oy' ; y'Ox đều bằng 90 độ

b) yOx' bằng 150 độ ; x'Oy' bằng 30 độ ; y'Ox bằng 150 độ 

Học tốt !

KHÓ QUÁ

a) Ta có: 

O1^ + O2^ = 180o (kề bù)

=> O1^ = 180o - O2^                        (1) 

và O3^ + O2^ = 180o (kề bù)

=> O3^ = 180o - O2^                         (2)

Từ (1) và (2) => O1^ = O3^  (hay xOy^ = x'Oy'^)

b) 

Ta có: 

O1^ + O2^ = 180o (kề bù)

=> O2^ = 180o - O1^                        (3) 

và O1^ + O4^ = 180o (kề bù)

=> O4^ = 180o - O1^                         (4)

Từ (3) và (4) => O2^ = O4^  (hay yOx'^ = xOy'^)

a)Góc xOy và xOy' là 2 góc kề bù

=>xOy+xOy'=180^o (1)

Góc xOy' và x'Oy' là 2 góc kề bù

=>xOy'+x'Oy'=180^o (2)

So sánh (1) và (2) ta có: 

xOy+xOy'=xOy'+x'Oy' (3)

Từ (3) => xOy=x'Oy'

b) Chứng minh tương tự phần a thôi :)

Góc xOy và yOx' là 2 góc kề bù

=>xOy+yOx'=180⁰ (1)

Góc xOy và xOy' là 2 góc kề bù

=>xOy+xOy'=180^o (2)

So sánh (1) và (2) ta có:

xOy+yOx'=xOy+xOy' (3)

Từ (3) => yOx'=xOy'

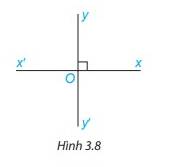
Góc x’Oy’ và xOy là hai góc đối đỉnh nên \(\widehat {x'Oy'} = \widehat {xOy} = 90^\circ \)

Góc xOy’ và xOy là hai góc kề bù nên

\(\begin{array}{l}\widehat {xOy'} + \widehat {xOy} = 180^\circ \\ \Rightarrow \widehat {xOy'} + 90^\circ  = 180^\circ \\ \Rightarrow \widehat {xOy'} = 180^\circ  - 90^\circ  = 90^\circ \end{array}\)

Góc x’Oy và xOy là hai góc kề bù nên

\(\begin{array}{l}\widehat {x'Oy} + \widehat {xOy} = 180^\circ \\ \Rightarrow \widehat {x'Oy} + 90^\circ  = 180^\circ \\ \Rightarrow \widehat {x'Oy} = 180^\circ  - 90^\circ  = 90^\circ \end{array}\)

Các góc đó đều có số đo bằng  90 °