Cho tam giác ABC đều, một điểm E thuộc BC trong nửa mặt phẳng bờ là đường thẳng BC không chứa A, dựng tia Bx sao cho \(\stackrel\frown{CBx}=\stackrel\frown{CAE}\) . Tia Bx cắt tia AE tại D. Chứng minh DA= DB+ DC.

Những câu hỏi liên quan
tam giác ABC đều , E thuộc BC . Trên nửa mặt phẳng bờ chứa tia BC ko chứa A , vẽ tia Bx sao cho CBx = CAE . Bx cắt tia AE tại D . CMR :
DA = DB + DC
Cho tam giác ABC đều và D là một điểm thuộc cạnh BC. Trên nửa mặt phẳng bờ BC không chứa điểm A; vẽ tia Bx sao cho góc CBx = góc CAD. Tia Bx cắt tia AD tại E. Chứng minh rằng EA = EB + EC. Mk cần gấp ! Cảm ơn trước nhé !
Không thể nào có chuyện EA = EB + EC. Nếu là chứng minh AD = BE + Ex thì mình làm được chứ cái đề như vậy là mình bó tay
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác ABC đều và D là một điểm thuộc cạnh BC.Trên nửa mặt phẳng bờ BC không chứ điểm A;Vẽ tia Bx sao cho CBx=CAD.Tia Bx cắt tia AD tại E.Chứng minh rằng EA=EB+EC
Cho tam giác cân abc gọi d là 1 điểm trên cạnh bc trên nửa mặt phẳng bờ bc không chứa điểm A kẻ tia Bx sao cho CBx = CAD , tia Bx cắt AD ở E . CMR tích AD x AE không đổi khi D thay đổi trên BC
cái đề em biết rồi chị nhắn tên bài cho em nhé là em giúp chị
Xét tg ACD và tg BED có
^ADC = ^BDE (góc đối đỉnh)
^CAD = ^CBE (đề bài)
=> ^ACB = ^AEB => C và E cùng nhìn AB dưới 1 góc = nhau và = ^ACB không đổi
=> A;B;E;C cùng nằm trên 1 đường tròn cố định (Do A;B;C cố định)
Từ A kẻ đường thẳng vuông góc với BC cắt BC tại H và đường tròn ngoại tiếp tứ giác ABEC tại F
Do ABC cân tại A => AF cũng là đường trung trực thuộc cạnh BC của tg ABC => Tâm đường tròn ngoại tiếp tứ giác AABEA thuộc AF => AF là đường kính của đường tròn ngoại tiếp tứ giác ABEC.
Nối E với F => ^AEF = 90 (góc nội tiếp chắn nửa đường tròn)
Xét tg vuông AHD và tg vuông AEF có
^EAF chung
=> tg AHD đồng dạng với tg AEF nên \(\frac{AD}{AF}=\frac{AH}{AE}\Rightarrow AD.AE=AH.AF\)
Do A,B,C cố định => AH không đổi
Do đường tròn ngoại tiếp tứ giác ABEC cố định => AF không đổi
=> AD.AE=AH.AF không đổi
Cho tam giác ABC Đều , E thuộc cạnh BC .Trên mp ko chứ A , dựng tai Bx sao cho góc CBx = góc CAE .Tia Bx cắt AE tại D
Chứng minh : DA=DB+DC
\(\text{Trên đoạn AD lấy E sao cho : BD=EF}\)
\(\Delta BED\text{có :}\)\(\widehat{EBD}+\widehat{BDE}+\widehat{DEB}=180^O\)
\(\Rightarrow\widehat{BDE}=180^O-\widehat{EBD}-\widehat{DEB}\)
\(\Rightarrow\widehat{BDE}=180^O-\widehat{CAE}-\widehat{AEC}\left(\widehat{DEB}=\widehat{AEC}\left(đ^2\right)\right)\)
\(\widehat{BDE}=\widehat{ACE}=60^O\)
\(\text{Vì BD=EF}\)\(\widehat{BDF}=60^o\)
\(\Rightarrow\Delta BDF\text{ là tam giác đều}\)
\(\Rightarrow BD=BF=FD\)
\(\text{ta có :}\)\(\widehat{ABF}=60^O-\widehat{FBE}\)
\(\widehat{EBD}=60^o-\widehat{FBE}\)
\(\Rightarrow\widehat{ABF}=\widehat{EBD}\)
\(\text{Xét :}\)\(\Delta ABF\text{ và }\)\(\Delta CBD\text{ có}:\)
\(AB=AC\left(gt\right)\)
\(\widehat{ABF}=\widehat{EBD}\left(cmt\right)\)
\(BF=BD\left(cmt\right)\)
\(\Rightarrow\Delta ABF=\Delta CBD\left(c.g.c\right)\)
\(\Rightarrow AF=DC\)
\(\text{ta có : AF+FD=AD}\)
\(\Rightarrow DC+BD=AD\left(đpcm\right)\)
Cho tam giác cân ABC(BA=BC),B=80 độ.Trên nửa mặt phẳng chứa điểm A có bờ là BC vẽ tia Bx sao cho CBx=10 độ.Trên tia Bx lấy E sao cho AE=AB.Trong tam giác ABE dựng tam giác đều MBE.
a, Chứng minh tam giác ABM=tam giác AEM
b, tính số đo góc BEC
c,chứng minh CE vuông góc với BM
Cho ΔABC đều và D là một điểm thuộc cạnh BC. Trên nửa mặt phẳng bờ BC không chứa điểm A, vẽ tia Bx sao cho \(\widehat{CBx} = \widehat{CAD}\). Tia Bx cắt tia AD tại E. Chứng minh rằng: EA = EB + EC.
Cho Tam giác ABC,vẽ tia Bx là tia phân giác của góc ABC.Tia Bx cắt đoạn thẳng AC tại D.Vẽ tia Dy song song AB,Dy cắt BC tại E.Vẽ tia Et song song Bx (Et thuộc nửa mặt phẳng có bờ là đường thẳng BC chứa điểm A).Chứng minh rằng:Et là tia phân giác của góc CED
cho em xin câu tl gấp ạ !!!!!!!
Cho tam giác ABC. Trên nửa mặt phẳng không chứa điểm C có bờ là đường thẳng AB, vẽ tia AD sao cho
B
A
D
^
A
B
C
^
. Trên nửa mặt phẳng không chứa điểm B có bờ là đường thẳng AC, vẽ tia AE sao cho
C
A
E
^
A
C
B...
Đọc tiếp
Cho tam giác ABC. Trên nửa mặt phẳng không chứa điểm C có bờ là đường thẳng AB, vẽ tia AD sao cho B A D ^ = A B C ^ . Trên nửa mặt phẳng không chứa điểm B có bờ là đường thẳng AC, vẽ tia AE sao cho C A E ^ = A C B ^ . Chứng minh.:
a) AD song song với BC;
b) Ba điểm D, A, E thẳng hàng
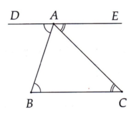
a) Có B A D ^ = A B C ^ ( giả thiết),
Mà hai góc ở vị trí so le trong nên AD // BC (theo tính chất hai đường thẳng song song).
b) Tương tự ý a), chứng minh được AE // BC
Theo tiên đề ơ-clit, hai đường thẳng AE và AD trùng nhau. Từ đó ba điểmD, A, E thẳng hàng.
Đúng 1
Bình luận (0)
















