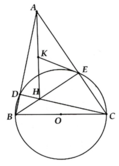
Cho tam giác ABC nội tiếp đường tròn tâm O . Phân giác góc BAC cắt đường tròn tâm O ở M . Tiếp tuyến kẻ từ M bới đường tròn cắt các tia AB và AC lần lượt ở D và E . Chứng minh :
a, BC // DE
b, \(\Delta\)AMB và \(\Delta\)MCE đồng dạng , \(\Delta\)AMC và \(\Delta\)MDB đồng dạng
c, Nếu AC=CE thì MA\(^2\)=MD.ME