giải phương trình sau
a. y3 - y2 - 21y +45 = 0
Giải hệ phương trình x 3 + 4 y = y 3 + 16 x 1 + y 2 = 5 ( 1 + x 2 )
x 3 + 4 y = y 3 + 16 x 1 + y 2 = 5 ( 1 + x 2 ) ( 1 )
– Xét x = 0, hệ (I) trở thành 4 y = y 3 y 2 = 4 < = > y = ± 2
– Xét x ≠ 0, đặt y x = t < = > y = x t . Hệ (I) trở thành
x 3 + 4 x t = x 3 t 3 + 16 x 1 + x 2 t 2 = 5 ( 1 + x 2 ) < = > x 3 ( t 3 − 1 ) = 4 x t − 16 x x 2 ( t 2 − 5 ) = 4 < = > x 3 ( t 3 − 1 ) = 4 x ( t − 4 ) ( 1 ) 4 = x 2 ( t 2 − 5 ) ( 2 )
Nhân từng vế của (1) và (2), ta được phương trình hệ quả
4 x 3 ( t 3 − 1 ) = 4 x 3 ( t − 4 ) ( t 2 − 5 ) < = > t 3 − 1 = t 3 − 4 t 2 − 5 t + 20 (Do x ≠ 0) <=>4t 2 + 5 t − 21 = 0 < = > t = − 3 t = 7 4
+ Với t = – 3, thay vào (2) được x2 = 1 ⇔ x = ±1.
x = 1 thì y = –3, thử lại (1;–3) là một nghiệm của (I)
x = –1 thì y = 3, thử lại (–1;3) là một nghiệm của (I)
+ Với t = 7/4 , thay vào (2) được x 2 = − 64 31 (loại)
Vậy hệ (I) có các nghiệm (0;2), (0;–2), (1;–3), (–1;3).
Hỏi có bao nhiêu giá trị nguyên của m để hệ phương trình sau có nghiệm:
x 3 - y 3 + 3 y 2 - 3 x - 2 = 0 1 x 2 + 1 - x 2 - 3 2 y - y 2 + m = 0 2
A. 1
B. 3
C. 2
D. 4
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 10 x - 9 y = 8 15 x + 21 y = 0 , 5
*Giải phương trình:
a, y2 + 7y + 2 = 0
b, y3 - y2 - 21y + 45 = 0
c, 2y3 - 5y2 + 8y - 3 = 0
d, (y+3)2 + (y+5)2 = 0
-giải giúp mk vs!! Mơn trc
Giải các hệ phương trình sau bằng phương pháp thế: x 2 - y 3 = 1 x + y 3 = 2
Cách 1
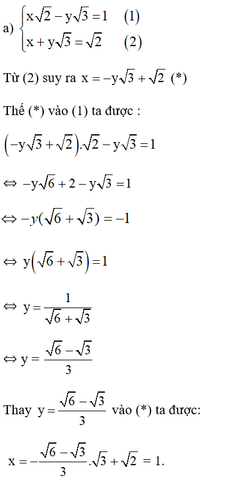
Vậy hệ phương trình có nghiệm duy nhất 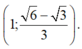
Cách 2
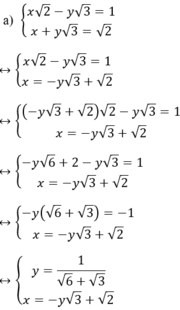

giải hệ phương trình : \(\hept{\begin{cases}14x^2-21y^2+22x-39y=0\\35x^2+28y^2+111x-10y=0\end{cases}}\)
Giải các hệ phương trình sau bằng phương pháp thế:
a ) x 2 − y 3 = 1 x + y 3 = 2 b ) x − 2 2 y = 5 x 2 + y = 1 − 10 c ) ( 2 − 1 ) x − y = 2 x + ( 2 + 1 ) y = 1
Cách 1
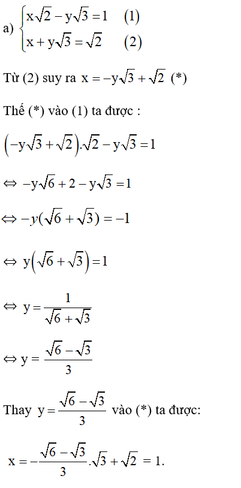
Vậy hệ phương trình có nghiệm duy nhất 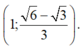
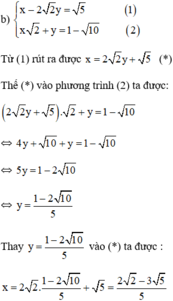
Vậy hệ phương trình có nghiệm duy nhất 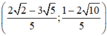
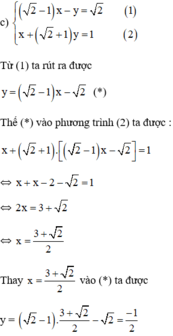
Vậy hệ phương trình có nghiệm duy nhất 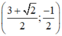
Cách 2
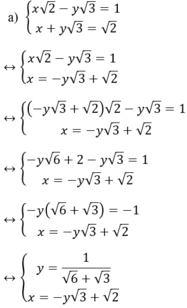

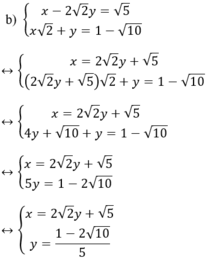

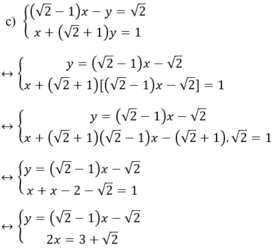

Kiến thức áp dụng
Giải hệ phương trình ta làm như sau:
Bước 1: Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
y2 – 8y + 16 = 0
Phương trình bậc hai y2 – 8y + 16 = 0
Có a = 1; b = -8; c = 16; Δ = b2 – 4ac = (-8)2 – 4.1.16 = 0.
Áp dụng công thức nghiệm ta có phương trình có nghiệm kép :
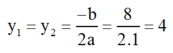
Vậy phương trình có nghiệm kép y = 4.
*Giải phương trình:
a, y2 + 7y + 2 = 0
b, y3 - y2 - 21y + 45 = 0
c, 2y3 - 5y2 + 8y - 3 = 0
d, (y+3)2 + (y+5)2 = 0
-giải giúp mk vs!! Mơn trc
d) Ta có: \(\left(y+3\right)^2\ge0\forall y\)
\(\left(y+5\right)^2\ge0\forall y\)
Do đó: \(\left(y+3\right)^2+\left(y+5\right)^2\ge0\forall y\)
mà \(\left(y+3\right)^2+\left(y+5\right)^2=0\)
nên \(\left\{{}\begin{matrix}\left(y+3\right)^2=0\\\left(y+5\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y+3=0\\y+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-3\\y=-5\end{matrix}\right.\)
Vậy: y=-3 và y=-5
a, y2 + 7y + 2 = 0
⇔ y(y + 7) + 2 = 0
⇔ y = \(-\frac{7-\sqrt{41}}{2}\) ; \(-\frac{7+\sqrt{41}}{2}\)
*(Nâng cao): - 0.29843788... ; - 6.70156211...
Vậy y = \(-\frac{7-\sqrt{41}}{2}\) ; \(-\frac{7+\sqrt{41}}{2}\).
Chúc bạn học tốt!