Câu a

Xét tam giác ABD và AMD có

AB = AM từ gt

Góc BAD = MAD vì AD phân giác BAM

AD chung

=> 2 tam guacs bằng nhau

Câu b

Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD

Bd = bm vì 2 tam giác ở câu a bằng nhau

Góc BDE bằng MDC đối đỉnh

=> 2 tam giác bằng nhau

Câu 4: 

a: Xét ΔABD vuông tại B và ΔAED vuông tại E có

AD chung

góc BAD=góc EAD

Do đó: ΔBAD=ΔEAD
b: Ta có: AB=AE

DB=DE

Do đó: AD là đường trung trực của BE

c: Xét ΔBDF vuông tại B và ΔEDC vuông tại E có

DB=DE

góc BDF=góc EDC

Do đó: ΔBDF=ΔEDC

Suy ra: BF=EC

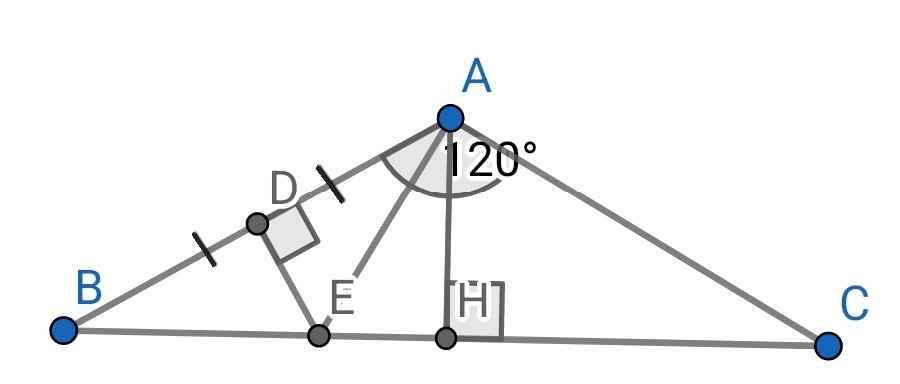 Do ∆ABC cân tại A (gt)

⇒ ∠B = ∠C = (180⁰ - ∠BAC) : 2

= (180⁰ - 120⁰) : 2

= 30⁰

∆AHB vuông tại H (do AH ⊥ BC)

⇒ ∠B + ∠BAH = 90⁰

⇒ ∠BAH = 90⁰ - ∠B

= 90⁰ - 30⁰

= 60⁰

Xét hai tam giác vuông: ∆AED và ∆BED có:

ED là cạnh chung

AD = BD (do D là trung điểm của AB)

⇒ ∆AED = ∆BED (hai cạnh góc vuông)

⇒ ∠EAD = ∠EBD = 30⁰ (hai góc tương ứng)

⇒ ∠EAH = ∠BAH - ∠EAD

= 60⁰ - 30⁰

= 30⁰

⇒ ∠EAH = ∠EAD

Xét hai tam giác vuông: ∆AEH và ∆AED có:

AE là cạnh chung

∠EAH = ∠EAD = 30⁰

⇒ ∆AEH = ∆AED (cạnh huyền - góc nhọn)

Mà ∆AED = ∆BED (cmt)

⇒ ∆BED = ∆AEH

a: Xét ΔABE vuông tại A và ΔHBE vuông tại H có

BE chung

\(\widehat{ABE}=\widehat{HBE}\)

Do đó: ΔABE=ΔHBE

b: ta có: ΔABE=ΔHBE

nên AE=HE; BA=BH

Suy ra: BE là đường trung trực của AH

a, Xét tam giác ABE và tam giác HBE có

                AB=HB(gt)

               \(\widehat{ABE}\)=\(\widehat{HBE}\)(gt)

                BE chung

\(\Rightarrow\)\(\Delta\)ABE=\(\Delta\)HBE(c.g.c)\(\Rightarrow\)\(\widehat{EAB}\)=\(\widehat{EHB}\)mà \(\widehat{EAB}\)=90 độ\(\Rightarrow\)\(\widehat{EHB}\)=90 độ

\(\Rightarrow\)EH vuông góc vs BC

a) Vì BE là tia phân giác của tam giác ABC

=> \(\widehat{ABE}=\widehat{EBC}\)hay \(\widehat{ABE}=\widehat{EBH}\)

* Xét tam giác ABE và tam giác HBE có :

 + )BA = BH ( gt)

+) \(\widehat{ABE}=\widehat{EBH}\)  (cmt)

+)BE chung

=> tam giác ABE = tam giác HBE ( c-g-c)

-> \(\widehat{BAE}=\widehat{BHE}\)( hai cạnh tương ứng )

Mà \(\widehat{BAE}=90^0\)( \(\widehat{BAC}=90^0\))

-> \(\widehat{BHE}=90^0\)

=> BH vuông góc EH hay BC vuông góc EH ( đpcm)

b) Vì tam giác ABE = tam giác HBE (cmt)

=> AE = EH ( 2 cạnh tương ứng )

* Có : AE = EH ( cmt)

=> Khoảng cách từ điểm E đến H bằng khoảng cách từ điểm E đến A ( 1)

BA = BH ( gt )

=. Khoản cách từ điểm B đến điềm H bằng khoảng cách từ điểm B đến điểm A ( 2 )

Từ ( 1 ) và ( 2 ) => BE là đường trung trực của AH ( đpcm )

c) Vì tam giác ABC có \(\widehat{A}\)= \(90^0\) ( gt)

=> AB vuông góc AC hay AE vuông góc AK ( E e AC ; K e AB )

=>\(\widehat{EAK}=90^0\)

Vì EH vuông góc AC ( cmt)

=> \(\widehat{EHC}=90^0\)

Xét tam giác AEK và tam giác HEC có 

AE = EH (cmt)

\(\widehat{EAK}=\widehat{EHC}=90^0\)

\(\widehat{AEK}=\widehat{HEC}\)(đối đỉnh)

=> tam giác AEK = tam giác HEC ( g-c-g)

=> EK = EC ( 2 cạnh tương ứng)

d) Có : BA = BH ( gt 0

=> tam giác BAH cân tại B

=. \(\widehat{BAH}=\frac{180^0-\widehat{ABH}}{2}\)( 3)

Vì tam giác AEK = tam giác HEC ( cmt )

=> AK = HC ( 2 cạnh tương ứng)

Có: AK = BA + AK

      BC = BH + HC

Mà BA = BH ( gt )

AK = HC ( cmt)

=> BK = BC

=> Tam giác BKC cân tại B

=>\(\widehat{BKC}=\frac{180^0-\widehat{KBC}}{2}\)hay \(\widehat{BKC}=\frac{180^0-\widehat{ABH}}{^{ }2}\)( 4 )

Từ ( 3 ) và ( 4 ) => \(\widehat{BAH}=\widehat{BKC}\)

Mà 2 góc ở vị trí đồng vị

=> AH // BC ( đpcm)

e) Có :  Tam giác BKC cân tại B

M là trung điểm BC 

=> BM là đường trung tuyến đồng thời là đường phân giác của tam giác BKC

Có BK là đường phân giác của tam giác BKC (cmt)

=> BK là đường phân giác của\(\widehat{KBC}\)hay \(\widehat{BAH}\)

Mà BE cũng là đường phân giác của \(\widehat{BAH}\)

=> BE trùng BK hay ba điểm B ; E ; K thẳng hàng ( đpcm)