B1 + B2 ạ

Những câu hỏi liên quan
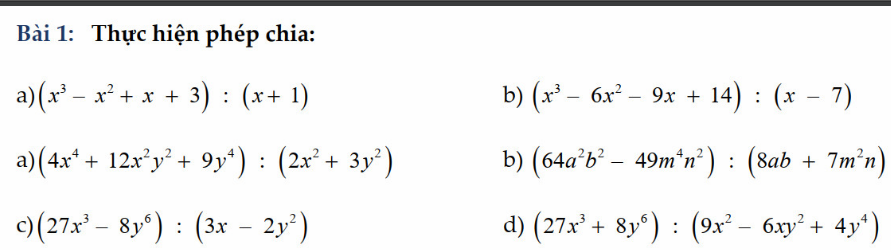 ghi là a1,a2,b1,b2 giúp e ạ
ghi là a1,a2,b1,b2 giúp e ạ
\(a_1,=\left(x^3+x^2-2x^2-2x+3x+3\right):\left(x+1\right)\\ =\left(x+1\right)\left(x^2-2x+3\right):\left(x+1\right)\\ =x^2-2x+3\\ a_2,=\left(2x^2+3y^2\right)^2:\left(2x^2+3y^2\right)=2x^2+3y^2\\ b_1,=\left(x^3-7x^2+x^2-7x-2x+14\right):\left(x-7\right)\\ =\left(x-7\right)\left(x^2+x-2\right):\left(x-7\right)\\ =x^2+x-2\\ b_2,=\left(8ab-7m^2n\right)\left(8ab+7m^2n\right):\left(8ab+7m^2n\right)=8ab-7m^2n\\ c,=\left(3x-2y^2\right)\left(9x^2+6xy^2+4y^4\right):\left(3x-2y^2\right)\\ =9x^2+6xy^2+4y^4\\ d,=\left(3x+2y^2\right)\left(9x^2-6xy^2+4y^4\right):\left(9x^2-6xy^2+4y^4\right)\\ =3x+2y^2\)
Đúng 0
Bình luận (0)

giúp mình b2 với ạ, b1 mình lm r, cảm ơnnn!!
Bài 2:
\(A=2+2^2+2^3+...+2^{60}\)
\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{59}+2^{60}\right)\)
\(A=2\cdot\left(1+2\right)+2^3\cdot\left(1+2\right)+...+2^{59}\cdot\left(1+2\right)\)
\(A=2\cdot3+2^3\cdot3+...+2^{59}\cdot3\)
\(A=3\cdot\left(2+2^3+...+2^{59}\right)\) ⋮ 3
Vậy: A ⋮ 3
_____________
\(A=2+2^2+...+2^{60}\)
\(A=\left(2+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{58}+2^{59}+2^{60}\right)\)
\(A=2\cdot\left(1+2+4\right)+2^4\cdot\left(1+2+4\right)+...+2^{58}\cdot\left(1+2+4\right)\)
\(A=2\cdot7+2^4\cdot7+...+2^{58}\cdot7\)
\(A=7\cdot\left(2+2^4+....+2^{58}\right)\) ⋮ 7
Vậy: A ⋮ 7
___________________
\(A=2+2^2+...+2^{60}\)
\(A=\left(2+2^3\right)+\left(2^2+2^4\right)+...+\left(2^{58}+2^{60}\right)\)
\(A=2\cdot\left(1+4\right)+2^2\cdot\left(1+4\right)+...+2^{58}\cdot\left(1+4\right)\)
\(A=2\cdot5+2^2\cdot5+...+2^{58}\cdot5\)
\(A=5\cdot\left(2+2^2+...+2^{58}\right)\) ⋮ 5
Vậy: A ⋮ 5
Đúng 2
Bình luận (1)
Nếu a1b1=a2b2 thì: A. a1/a2=b1/b2 B. a1/a2=b2/b1 C. a1/b2=a2/b1 D. a1/b2=b1/a2
GYE4F4GGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGG
Đúng 0
Bình luận (0)
Mn giúp em B1 + B2 vs ạ !!! Mai em phải nộp r 😭😭
Cho a1; a2; b1; b2 là 4 số dương có a1.a2=b1.b2
CMR: (a1/b1)+(a2/b2)>=2
Dễ vậy mà ko làm đc àk
\(a_1.a_2=b_1.b_2\Rightarrow\frac{a_1}{b_1}=\frac{b_2}{a_2}\)
\(\Rightarrow\frac{a_1}{b_1}+\frac{a_2}{b_2}=\frac{b_2}{a_2}+\frac{a_2}{b_2}\ge2\sqrt{\frac{b_2}{a_2}.\frac{a_2}{b_2}}=2\) (AM - GM)
Đúng 0
Bình luận (0)
có a1.a2=b1.b2
=> a1/b1=b2/a2
có \(\frac{a1}{b1}+\frac{a2}{b2}=\frac{b2}{a2}+\frac{a2}{b2}\)
áp dụng bất đẳng thức cosi cho 2 số dương có
\(\frac{b2}{a2}+\frac{a2}{b2}\ge2\sqrt{\frac{b2}{a2}.\left(\frac{a2}{b2}\right)}=2\)(đpcm)
Đúng 0
Bình luận (0)
Trên trang tính, tại ô A1=7; B1=9; A2=3; B2=2; tại C2 có công thức: =Min(A2,B2), sao chép công thức từ ô C2 sang ô C1, thì ô C1 sẽ có công thức là
=Min(A1,B1)
=Min(A2,B1)
=Min(A1,B2)
=Min(A2,B2)
B1: a)|x-1/2|+1/2=x b) |1-3x|+1=3x B2: rút gọn a) C=|5-x|+x B)D=|2x-1|-x Giúp mình với ạ
Bài 1:
a: \(\left|x-\dfrac{1}{2}\right|+\dfrac{1}{2}=x\)
=>\(\left|x-\dfrac{1}{2}\right|=x-\dfrac{1}{2}\)
=>\(x-\dfrac{1}{2}>=0\)
=>\(x>=\dfrac{1}{2}\)
b: \(\left|1-3x\right|+1=3x\)
=>\(\left|1-3x\right|=3x-1\)
=>\(1-3x< =0\)
=>3x-1>=0
=>3x>=1
=>\(x>=\dfrac{1}{3}\)
Bài 2:
a: \(C=\left|5-x\right|+x=\left|x-5\right|+x\)
TH1: x>=5
\(C=x-5+x=2x-5\)
TH2: x<5
C=5-x+x=5
b: D=|2x-1|-x
TH1: x>=1/2
\(D=2x-1-x=x-1\)
TH2: \(x< \dfrac{1}{2}\)
D=1-2x-x=1-3x
Đúng 2
Bình luận (0)
Với A1=10, A2=30, A3=20, B1=20, B2=40, B3=50, B4=100
Tính kết quả:
a) = AVERAGE(SUM(B1, B2, B3)
b) = SUM(A1, B1, B4)
c) = MAX(A1, B1, B4)
d) = SUM( AVERAGE(B1:B4)
a) \(\approx\) 36,6
b) 130
c) 100
Đúng 0
Bình luận (0)
Cho các số thực dương a1,b1,c1,a2,b2,c2 thỏa mãn điều kiện \(\frac{a1}{a2}=\frac{b1}{b2}=\frac{c1}{c2}\).CMR \(\sqrt{\left(a1+b1+c1\right)\left(a2+b2+c2\right)}=\sqrt{a1a2}+\sqrt{b1b2}+\sqrt{c1c2}\)
a1/a2 = b1/b2 = c1/c2 = k
a1=k.a2, b1=k.b2, c1=k.c2
Biểu thức trở thành
√(k.a2 + k.b2 + k.c2).(a2 + b2 + c2)= √k.a2.a2 + √k.b2.b2 + √k.c2.c2
√k.(a2+b2+c2)2 = a2. √k + b2. √k + c2. √k
(a2+b2+c2). √k = (a2+b2+c2). √k (hiển nhiên đúng)
Suy ra điều phải chứng minh
Đúng 0
Bình luận (0)





















