nêu tính chất các trường hợp bằng nhau của hai tam giác (c.c.c); (c.g.c); (g.c.g)

Những câu hỏi liên quan
1. hai tam giác bằng nhau là hai tam giác như thế nào?
2.có mấy trường hợp bằng nhau của hai tam giác? Nêu các trường hợp đó.
3.nêu các trường hợp bằng nhau của hai tam giác vuông.
4.phát biểu định nghĩa và tính chất tam giác cân. Nêu các cách chứng minh một tam giác là tam giác cân.
5.phát biểu định nghĩa và tính chất tam giác đều.Nêu các cách chưng minh một tam giác là tam giác đều.
6.phát biểu định lí Py-ta-go thuận và đảo.
Đọc tiếp
1. hai tam giác bằng nhau là hai tam giác như thế nào?
2.có mấy trường hợp bằng nhau của hai tam giác? Nêu các trường hợp đó.
3.nêu các trường hợp bằng nhau của hai tam giác vuông.
4.phát biểu định nghĩa và tính chất tam giác cân. Nêu các cách chứng minh một tam giác là tam giác cân.
5.phát biểu định nghĩa và tính chất tam giác đều.Nêu các cách chưng minh một tam giác là tam giác đều.
6.phát biểu định lí Py-ta-go thuận và đảo.
1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông
Đúng 0
Bình luận (0)
1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông
Đúng 0
Bình luận (0)
Nêu các trường hợp bằng nhau của hai tam giác, hai tam giác vuông? Vẽ hình, ghi giảthuyết, kết luận cho từng trường hợp?2. Nêu định nghĩa, tính chất của tam giác cân, tam giác đều?3. Nêu định lý Pytago thuận và đảo, vẽ hình, ghi giả thuyết, kết luận của cả hai định lý4. Nêu định lý về quan hệ giữa góc và cạnh đối diện trong tam giác, vẽ hình, ghi giả thiết, kết luận.5. Nêu quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu, vẽ hình, ghigiả thuyết, kết luận cho từng mối quan hệ....
Đọc tiếp
Nêu các trường hợp bằng nhau của hai tam giác, hai tam giác vuông?
Vẽ hình, ghi giảthuyết, kết luận cho từng trường hợp?
2. Nêu định nghĩa, tính chất của tam giác cân, tam giác đều?
3. Nêu định lý Pytago thuận và đảo, vẽ hình, ghi giả thuyết, kết luận của cả hai định lý
4. Nêu định lý về quan hệ giữa góc và cạnh đối diện trong tam giác, vẽ hình, ghi giả thiết, kết luận.
5. Nêu quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu, vẽ hình, ghigiả thuyết, kết luận cho từng mối quan hệ.
6. Nêu định lý về bất đẳng thức trong tam giác, vẽ hình, ghi giả thiết, kết luận
- Nêu các trường hợp bằng nhau của hai tam giác.- Nêu các trường hợp bằng nhau của hai tam giác vuông.- Thế nào là tam giác cân? Nêu các tính chất của tam giác cân? Nêu các cách để chứng minh tam giác cân- Thế nào là tam giác vuông cân? Nêu các tính chất của tam giác vuông cân? Số đo mỗi góc nhọn trong tam giác vuông cân là bao nhiêu?Thế nào là tam giác đều? Nêu các tính chất
Đọc tiếp
- Nêu các trường hợp bằng nhau của hai tam giác.
- Nêu các trường hợp bằng nhau của hai tam giác vuông.
- Thế nào là tam giác cân? Nêu các tính chất của tam giác cân? Nêu các cách để chứng minh tam giác cân
- Thế nào là tam giác vuông cân? Nêu các tính chất của tam giác vuông cân? Số đo mỗi góc nhọn trong tam giác vuông cân là bao nhiêu?
Thế nào là tam giác đều? Nêu các tính chất
Hãy nêu các trường hợp bằng nhau cho mỗi cặp tam giác trong Hình 17. Từ các điều kiện bằng nhau của hai tam giác, người ta suy ra được các trường hợp bằng nhau sau đây của hai tam giác vuông.
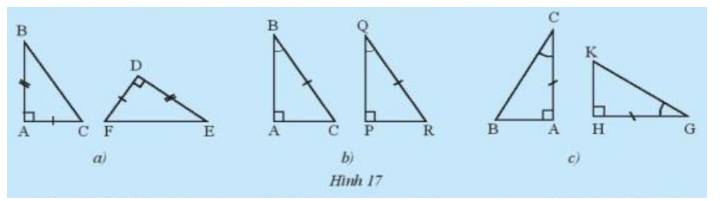
a) Xét \(\Delta{ABC}\) và \(\Delta{DEF}\) có:
AB = DE (gt)
\(\widehat {BAC} = \widehat {EDF}\) (gt)
AC = DF (gt)
\(\Rightarrow \Delta{ABC}=\Delta{DEF}\) (c-g-c)
b) Ta có: \(\widehat B + \widehat C = \widehat Q + \widehat R = 90^0\)
Mà \(\widehat B = \widehat Q\) \( \Rightarrow \widehat C = \widehat R\)
Xét \(\Delta{ABC}\) và \(\Delta{PQR}\) có:
\(\widehat C = \widehat R\) (gt)
BC = QR (gt)
\(\widehat B = \widehat Q\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{PQR}\) (g-c-g)
c) Xét \(\Delta{ABC}\) và \(\Delta{HKG}\) có:
\(\widehat C = \widehat G\) (gt)
AC = HG (gt)
\(\widehat A = \widehat H\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{HKG}\) (g-c-g)
Đúng 0
Bình luận (0)
1. Nêu các trường hợp bằng nhau của tam giác thường và tam giác vuông
( Viết bằng lời - Vẽ hình - Viết giả thiết , kết luận )
2. Nêu tính chất và góc của tam giác cân
Bài 1:
I. Trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh:
1) Vẽ tam giác biết độ dài 3 cạnh: (HS tự nêu các bước vẽ)
VD: Vẽ rABC biết AB = 3cm, BC = 5cm, AC = 4cm.
2) Trường hợp bằng nhau cạnh – cạnh – cạnh:
“Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.”
II. Trường hợp bằng nhau thứ nhất của tam giác cạnh – góc – cạnh:
1) Vẽ tam giác biết độ dài 2 cạnh và 1 góc xen giữa:
(HS tự nêu các bước vẽ)
VD: Vẽ rABC biết AB = BC = 4cm,
2) Trường hợp bằng nhau cạnh – góc – cạnh:
“Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.”

* Lưu ý: Cặp góc bằng nhau phải xen giữa hai cặp cạnh bằng nhau thì mới kết luận được hai tam giác bằng nhau.
III. Trường hợp bằng nhau thứ nhất của tam giác góc – cạnh – góc:
1) Vẽ tam giác biết độ dài 1 cạnh và 2 góc kề:
(HS tự nêu các bước vẽ)
VD: Vẽ rABC biết AC = 5cm,
2) Trường hợp bằng nhau góc – cạnh – góc:
“Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.”
Đúng 0
Bình luận (0)
* Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
* Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề ấy cạnh của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (g-c-g)
* Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (ch-gn)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cm 4 tam giác bằng nhau ở trường hợp c.c.c thì chúng ta có thể suy ra diện tích 4 tam giác đó bằng nhu được không ?
Các bạn làm giùm mình nhen
cho tam giác mnp và tam giác def có mn = de,pm = df. cần thêm điều kiện gì để tam giác mnp và tam giác def bằng nhau theo trường hợp ( c.c.c )
Để hai tam giác trên bằng nhau theo trường hợp c.c.c thì các cặp cạnh tương ứng phải bằng nhau. Vì đã có hai cặp cạnh tương ứng là MN và DE, PM và DF nên cần thêm điều kiện NP = EF để hai tam giác trên bằng nhau theo trường hợp c.c.c
Đúng 0
Bình luận (0)
- Phát biểu định nghĩa và tính chất tam giác cân. Nêu các cách chứng minh • các dụngm giác là tam giác cân.(5) Phát biểu định nghĩa và tính chất tam giác đều. Nêu các cách chứng minh tam giác là tam giác đều.(6) Phát biểu định lí Py-ta-go thuận và đảo. b) Trả lời các câu hỏi sau(1) Thế nào là hai tam giác bằng nhau? đến đo (2) Thế nào là tam giác cân?(3) Thế nào là tam giác vuông cân? (4) Thế nào là tam giác đều? (5) Nêu các tính chất của tam giác cân. (6) Nêu các tính chất của tam giác vuông câ...
Đọc tiếp
- Phát biểu định nghĩa và tính chất tam giác cân. Nêu các cách chứng minh • các dụng
m giác là tam giác cân.
(5) Phát biểu định nghĩa và tính chất tam giác đều. Nêu các cách chứng minh tam giác là tam giác đều.
(6) Phát biểu định lí Py-ta-go thuận và đảo. b) Trả lời các câu hỏi sau
(1) Thế nào là hai tam giác bằng nhau? đến đo (2) Thế nào là tam giác cân?
(3) Thế nào là tam giác vuông cân? (4) Thế nào là tam giác đều? (5) Nêu các tính chất của tam giác cân. (6) Nêu các tính chất của tam giác vuông cân. (7) Nêu các tính chất của tam giác đều. c) Đố bạn nêu chính xác các tính chất sau: (1) Nếu ba cạnh của tam giác này .... tam giác kia, thì hai tam giác đó bằng
(2) Nếu hai cạnh và góc xen giữa của tam giác này .... tam giác kia, thì giác đó bằng nhau.
(3) Nếu một cạnh và hai góc kề của tam giác này .... tam giác kia, thì hai ta đó bằng nhau.
(4) Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vụ .... tam giác vuông kia, thì hai tam giác đó bằng nhau.
(5) Nếu cạnh huyền và một góc nhọn của tam giác vuông này .... tam giá kia, thì hai tam giác đó bằng nhau. | (6) Nếu hai cạnh góc vuông của tam giác vuông này .... tam giác vuông ki tam giác đó bằng nhau.
6 tính chất tam giác vuông cân
(7) Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này .... vuông kia, thì hai tam giác đó bằng nhau.
(8) Trong một tam giác vuông, bình phương của cạnh huyền bằng... cạnh g (9) Nếu một tam giác có bình phương của một cạnh bằng... đó là tam gi
1/Nêu tính chất 2 góc đối đỉnh (1)
2/Nếu các trường hợp của 2 tam giác bằng nhau
3/Cho tam giác ABC, trung AM đồng thời là phân giác. Chứng minh tam giác ABC cân tại A.
1/ Hai góc đối đỉnh thì bằng nhau
2/ Trong tam giác thường: cạnh-canh-cạnh ; cạnh-góc-cạnh; góc-cạnh-góc
Trong tam giác vuông : cạnh huyền- góc nhọn; cạnh huyền-cạnh góc vuộng
3/ Xét \(\Delta ABM\) và \(\Delta ACM\) có:
BM= CM ( AM là đường trung trực)
Góc AMB = góc AMC = 90o
AM chung
-> \(\Delta ABM\)= \(\Delta ACM\) (c.g.c)
-> AB=AC(cạnh tương ứng)
-> Tam giác ABC cân tại A
3/
Đúng 0
Bình luận (0)


















