CMR:nếu 1 đthẳng song song với 1 dây thì tiếp tuyến chia đôi cung căng dây.Mn giúp mik vs ạg

Những câu hỏi liên quan
Cho đường tròn (O) đường kính AB. Vẽ 2 dây AM và BN song song sao cho sđ cung BM<90 độ. Vẽ dây MD song song với AB. Dây DN cắt AB tại F. Từ R vẽ 1 đường thẳng song song với AM cắt DM tại C. Chứng minh:
a, AB vuông góc DN
b, BC là tiếp tuyến của (O)
Từ một điểm S nằm ngoài đường tròn tâm O kẻ hai tiếp tuyến SA và SB (A và B là hai tiếp điểm). Một cát tuyến kẻ qua S cắt đường tròn tại C và D (C thuộc cung lớn AB; D thuộc cung nhỏ AB). Qua D kẻ dây DE song song với SA, cắt dây AB tại F. Gọi H là trung điểm dây DC. Chứng minh rằng HF song song với AC.
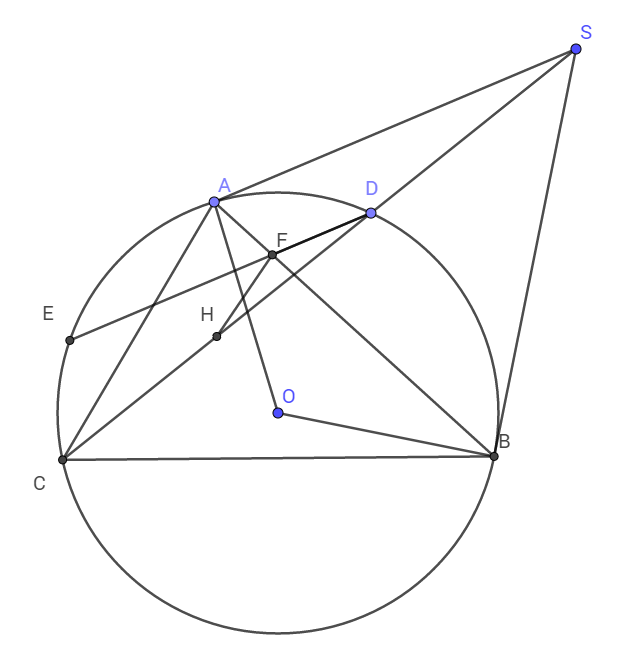
Ta có các tam giác vuông AOS; HOS, BOS có chung cạnh huyền OS nên S, A, H, O, B nội tiếp đường tròn đường kính OS.
Khi đó ta có :
\(\widehat{ASH}=\widehat{ABH}\) (Hai góc nội tiếp cùng chắn cung AH)
Mà \(\widehat{ASH}=\widehat{FDH}\) (Hai góc đồng vị)
\(\Rightarrow\widehat{ABH}=\widehat{FDH}\)
Suy ra tứ giác HFDO nội tiếp.
Từ đó ta có \(\widehat{FHD}=\widehat{ABD}\)(Hai góc nội tiếp)
Mà \(\widehat{ABD}=\widehat{ACD}\) (Hai góc nội tiếp)
Nên \(\widehat{FHD}=\widehat{ACD}\)
Chúng lại ở vị trí đồng vị nên HF // AC.
Đúng 0
Bình luận (0)
Cho đường tròn (O) đường kính AB. Vẽ 2 dây AM và BN song song sao cho sđ cung BM<90 độ. Vẽ dây MD song song với AB. Dây DN cắt AB tại F. Từ R vẽ 1 đường thẳng song song với AM cắt DM tại C. Chứng minh:
a, AB vuông góc DN
b, BC là tiếp tuyến của (O)
Cho (O) đường kính AB. Vẽ hai dây AM và BN song song với nhau sao cho Sđ cung BM<90°. Vẽ dây MD song song với AB. Dây DN cắt AB tại E. Từ E vẽ 1 đường thẳng // với AM cắt DM tại C. CMR:
a) AB vuông góc DN.
b) BC là tiếp tuyến (O).
Cho đường tròn (O) đường kính AC và điểm B trên nửa đường tròn sao cho sđ cung BC =60°. Qua B kẻ dây BD vuông góc AC, qua D kẻ dây DF song song AC.
a, Tính số đo các cung CD, AB, FD
b, Tìm tiếp tuyến của (O) song song với AB
a: Xét (O) có
ΔBAC nội tiếp
AC là đường kính
Do đó: ΔBAC vuông tại B
Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{BAC}=\dfrac{1}{2}\cdot sđ\stackrel\frown{BC}=\dfrac{1}{2}\cdot60^0=30^0\)
Gọi H là giao điểm của BD với AC
BD\(\perp\)AC nên BD\(\perp\)AC tại H
ΔOBD cân tại O
mà OH là đường cao
nên H là trung điểm của BD
Xét ΔCBD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCBD cân tại C
=>CB=CD
Xét ΔCOD và ΔCOB có
CD=CB
OD=OB
CO chung
Do đó: ΔCOD=ΔCOB
=>\(\widehat{COD}=\widehat{COB}\)
=>\(sđ\stackrel\frown{CB}=sđ\stackrel\frown{CD}=60^0\)
Xét ΔBAC vuông tại B có \(\widehat{BAC}+\widehat{BCA}=90^0\)
=>\(\widehat{BCA}+30^0=90^0\)
=>\(\widehat{BCA}=60^0\)
Xét (O) có
\(\widehat{BCA}\) là góc nội tiếp chắn cung AB
Do đó: \(\widehat{BCA}=\dfrac{1}{2}\cdot sđ\stackrel\frown{AB}\)
=>\(sđ\stackrel\frown{AB}=2\cdot\widehat{BCA}=120^0\)
DF//AC
DB\(\perp\)AC
Do đó: DF\(\perp\)DB
=>ΔDFB vuông tại D
ΔDFB vuông tại D
nên ΔDFB nội tiếp đường tròn đường kính BF
mà ΔDFB nội tiếp (O)
nên O là trung điểm của BF
=>OA//DF
=>\(\widehat{BFD}=\widehat{BOH}=\widehat{BOC}\)(hai góc đồng vị)
=>\(\widehat{BFD}=60^0\)
ΔBDF vuông tại D
=>\(\widehat{BFD}+\widehat{FBD}=90^0\)
=>\(\widehat{FBD}+60^0=90^0\)
=>\(\widehat{FBD}=30^0\)
Xét (O) có
\(\widehat{FBD}\) là góc nội tiếp chắn cung FD
Do đó: \(\widehat{FBD}=\dfrac{1}{2}\cdot sđ\stackrel\frown{FD}\)
=>\(sđ\stackrel\frown{FD}=2\cdot\widehat{FBD}=2\cdot\)30=60 độ
Đúng 1
Bình luận (0)
Cho đường tròn (O) , đường kính AB .Vẽ 2 dây AM và BM song song với nhau sao cho sđ cung BM < 90. . Vẽ dây MD song song với AB . Dây AN cắt AB tại E . Đường thẳng qua E song song với AM cắt DM tại C . Chứng minh rằng
a) Cung AD = cung AN và AB \(\perp\)DN
b) BC là tiếp tuyến của (O)
Cho (O) và 2 tiếp tuyến SA, SB. Kẻ dây cung BC. Đường kính vuông góc với AC cắt BC tại I. Chứng minh:
a) 4 điểm S, A, I, B thuộc 1 đường tròn
b) Tứ giác SAOI nội tiếp
c) SI song song với AC
Cho (O) và 2 tiếp tuyến SA, SB. Kẻ dây cung BC. Đường kính vuông góc với AC cắt BC tại I. Chứng minh:
a) 4 điểm S, A, I, B thuộc 1 đường tròn
b) Tứ giác SAOI nội tiếp
c) SI song song với AC
Cho (O) và 2 tiếp tuyến SA, SB. Kẻ dây cung BC. Đường kính vuông góc với AC cắt BC tại I. Chứng minh:
a) 4 điểm S, A, I, B thuộc 1 đường tròn
b) Tứ giác SAOI nội tiếp
c) SI song song với AC










