từ các chữ số 0,1,2,3,4,5 lập dc bn số chẵn có 4 chữ số đôi một khác nhau

Những câu hỏi liên quan
Từ các chữ số 0,1,2,3,4,5 có thể lập được bao nhiêu số tự nhiên: a) Có 3 chữ số khác nhau b) Có 3 chữ số chẵn khác nhau c) Có 3 chữ số lẻ khác nhau
a: \(\overline{abc}\)
a có 5 cách
b có 5 cách
c có 4 cách
=>Có 5*5*4=100 cách
b: \(\overline{abc}\)
a có 2 cách
b có 2 cách
c có 1 cách
=>Có 2*2*1=4 cách
c: \(\overline{abc}\)
a có 3 cách
b có 2 cách
c có 1 cách
=>Có 3*2*1=6 cách
Đúng 0
Bình luận (0)
Với các chữ số 0,1,2,3,4,5,có thể lập được bao nhiêu a, số lẻ gồm 4 chữ số khác nhau b, số chẵn gồm 4 chữ số khác nhau
Từ các chữ số 0,1,2,3,4,5 có thể lập được bao nhiêu số gồm 3 chữ số đôi một khác nhau không chia hết cho 9
1. Từ 0,1,2,3,4,5 có thể lập được số các số có 3 chữ số đôi một khác nhau và không chia hết cho 5 là
\(\overline{abc}\)
c có 4 cách
a có 4 cách
b có 3 cách
=>Có 4*4*3=48 cách
Đúng 0
Bình luận (0)
Cho tập A = {0,1,2,3,4,5}. Có bao nhiêu số tự nhiên chẵn gồm 4 chữ số đôi một khác nhau chia hết cho 10 lấy từ tập A
Có \(A^3_5=60\) số tự nhiên thỏa mãn yêu cầu bài toán.
Đúng 1
Bình luận (0)
Từ các chữ số 1,2,3,4,5,6,7 , lập được bao nhiêu số tự nhiên
a) Có 4 chữ số đôi một khác nhau?
b) Có 3 chữ số đôi một khác nhau và chia hết cho 9?
c) Là số chẵn và có 5 chữ số đôi một khác nhau?
d) Có 9 chữ số sao cho chữ số 1 có mặt 3 lần, các chữ số khác có mặt đúng một lần?
a: \(\overline{abcd}\)
a có 7 cách chọn
b có 6 cách
c có 5 cách
d có 4 cách
=>Có 7*6*5*4=840 cách
b: Bộ ba chia hết cho 9 sẽ có thể là (1;2;6); (1;3;5); (2;3;4)
Mỗi bộ có 3!=6(cách)
=>Có 6*3=18 cách
c: \(\overline{abcde}\)
e có 3 cách
a có 6 cách
b có 5 cách
c có 4 cách
d có 3 cách
=>Có 3*6*5*4*3=1080 cách
Đúng 0
Bình luận (0)
Từ các chữ số 0,1,2,3,4,5 có thể lập được bao nhiêu số tự nhiên thỏa mãn:
a. Có 5 chữ số khác nhau
b. Là số chẵn có 5 chữ số khác nhau
c. Có 5 chữ số khác nhau và chia hết cho 5
Số tự nhiên đó có dạng \(\overline{abcde}\)
a, a có 5 cách chọn.
b có 5 cách chọn.
c có 4 cách chọn.
d có 3 cách chọn.
e có 2 cách chọn.
\(\Rightarrow\) Có \(5.5.4.3.2=600\) số thỏa mãn.
b, TH1: \(e=0\)
a có 5 cách chọn.
b có 4 cách chọn.
c có 3 cách chọn.
d có 2 cách chọn.
\(\Rightarrow\) Có \(5.4.3.2=120\) số thỏa mãn.
TH2: \(e\ne0\)
a có 5 cách chọn.
e có 2 cách chọn.
b có 4 cách chọn.
c có 3 cách chọn.
d có 2 cách chọn.
\(\Rightarrow\) Có \(5.4.3.2.2=240\) số thỏa mãn.
Vậy có \(120+240=360\) số tự nhiên thỏa mãn yêu cầu bài toán.
c, TH1: \(e=0\Rightarrow\) có 120 số thỏa mãn.
TH2: \(e=5\)
a có 4 cách chọn.
b có 4 cách chọn.
c có 3 cách chọn.
d có 2 cách chọn.
\(\Rightarrow\) Có \(4.4.3.2=96\) số thỏa mãn.
Vậy có \(120+96=216\) số tự nhiên thỏa mãn yêu cầu bài toán.
Đúng 1
Bình luận (0)
Từ các số 0,1,2,3,4,5 có thể lập được:
c) Bao nhiêu số có ba chữ số ( không nhất thiết khác nhau) và là số chẵn?
A. 60
B. 90
C. 450
D. 100
Gọi tập hợp E = {0,1,2,3,4,5}
c) Số tự nhiên có 3 chữ số có dạng
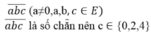
Có ba cách chọn chữ số c ( vì c ∈ {0,2,4}).
Ứng với mỗi cách chọn c , có 6 cách chọn chữ số b (vì b ∈ E)
ứng với mỗi cách chọn c, b có 5 cách chọn chữ số a (vì a ∈ E và a≠ 0)
Áp dụng quy tắc nhân ta có 3*6*5 = 90 số có 3 chữ số.
Vì vậy đáp án là B
Đúng 0
Bình luận (0)
có bao nhiêu số chẵn có 3 chữ số khác nhau được lập bởi các chữ số 0,1,2,3,4,5
Co 5 cach chon c/s hang tram
Co 5 cach chon c/s hang chuc
Co 3 cach chon c/s hang don vi
Vay lap dc:5*5*3=75(so)
olm duyet di
Đúng 0
Bình luận (0)
Số chẵn có chữ số tạn cùng là: 0, 2, 4.
Vậy chữ số tận cùng có 3 cách chọn.
Chữ số thứ 2 có 5 cách chọn.
Chữ số đầu tiên có 3 cách chọn (vì số 0 không thể đứng đầu)
Ta có
3x5x3=45 ( số)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời


















