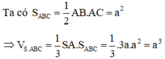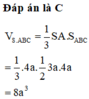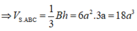Cho tam giác ABC vuông tại A có AB=3a; AC=4a. Khi đó độ dài của vectơ BC là bn?

Những câu hỏi liên quan
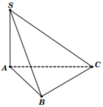
Cho tam giác ABC có AB 3a, đường cao CH a và AH a. Trên các đường thẳng vuông góc với mặt phẳng (ABC) tại A, B, C về cùng một phía của mặt phẳng (ABC) lấy các điểm A’, B’, C’sao cho AA’ 3a, BB’ 3a, CC’ a. Tính diện tích tam giác A’B’C’.
Đọc tiếp
Cho tam giác ABC có AB = 3a, đường cao CH = a và AH = a. Trên các đường thẳng vuông góc với mặt phẳng (ABC) tại A, B, C về cùng một phía của mặt phẳng (ABC) lấy các điểm A’, B’, C’sao cho AA’ = 3a, BB’ = 3a, CC’ = a. Tính diện tích tam giác A’B’C’.
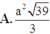
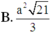
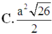

Đáp án D.
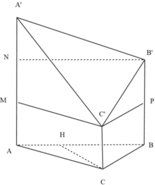
Trên AA’ lấy M và N sao cho AM = MN = NA’ = a; trên BB’ lấy điểm P sao cho BP = PB’ = a.
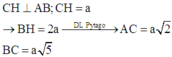
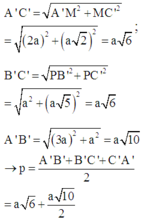
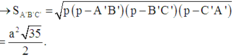
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 3a, AC = 4a. Khi đó độ dài vecto BC là
Lời giải:
$|\overrightarrow{BC}|=BC=\sqrt{AB^2+AC^2}=\sqrt{(3a)^2+(4a)^2}=5a$ theo định lý Pitago.
Đúng 2
Bình luận (0)
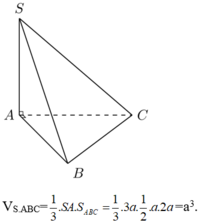
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với đáy và ABa, AC2a,SA3a. Tính thể tích khối chóp S.ABC. A. V6a3 B. Va3 C. V2a3 D. V3a3.
Đọc tiếp
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với đáy và AB=a, AC=2a,SA=3a. Tính thể tích khối chóp S.ABC.
A. V=6a3
B. V=a3
C. V=2a3
D. V=3a3.
cho tam giác ABC vuông tại A . Có AB 3a,AC 4a. Dựng và tính độ dài véctơ AB véctơ AC
Cho hình chóp S.ABC có tam giác ABC vuông tại A,
A
B
2
a
,
A
C
a
,
S
A
3
a
,
S
A
⊥
A
B
C
. Thể tích của hình chóp là A.
V
2
a...
Đọc tiếp
Cho hình chóp S.ABC có tam giác ABC vuông tại A, A B = 2 a , A C = a , S A = 3 a , S A ⊥ A B C . Thể tích của hình chóp là
A. V = 2 a 3
B. V = 6 a 3
C. V = a 3
D. V = 3 a 3
Cho hình chóp S.ABC có SA vuông góc với (ABC) tam giác ABC vuông tại A, AB=3a,AC=4a,SA=4a. Thể tích khối chóp S.ABC là:
A. 2 a 3
B. 6 a 3
C. 8 a 3
D. 9 a 3
Cho khối chóp S.ABC có SA vuông góc với (ABC), tam giác ABC vuông tại A, AB4a, ACSA3a. Tính thể tích của khối chóp S.ABC. A. 6
a
3
B. 8
a
3
C. 2
a
3
D. 9
a
3
Đọc tiếp
Cho khối chóp S.ABC có SA vuông góc với (ABC), tam giác ABC vuông tại A, AB=4a, AC=SA=3a. Tính thể tích của khối chóp S.ABC.
A. 6 a 3
B. 8 a 3
C. 2 a 3
D. 9 a 3
Cho khối chóp S.ABC có SA vuông góc với (ABC), tam giác ABC vuông tại A, AB=4a,
AC=SA=3a. Tính thể tích của khối chóp S.ABC.
A. 6 a 3
B. 8 a 3
C. 2 a 3
D. 9 a 3
cho tam giác ABC vuông tại A . Có AB = 3a,AC =4a. Dựng và tính độ dài véctơ AB +véctơ AC