Xác định các hằng số a và b sao cho x4+ax+b chia hết cho x2-1

Những câu hỏi liên quan
Xác định hằng số a và b sao cho ( x 4 + ax + b) ⁝ ( x 2 – 4)
A. a = 0 và b = -16
B. a = 0 và b = 16
C. a = 0 và b =0
D. a = 1 và b = 1
Ta có
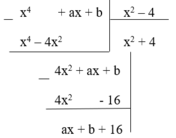
để x 4 + ax + b chia hết cho x 2 – 4 thì ax + b + 16 = 0
ó a x = 0 b + 16 = 0 ó a = 0 b = - 16
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Xác định số hữu tỉ a, b sao cho:
a) 2x2 + ax - 4 chia hết cho x + 4
b) x4 - 3x3 + 3x2 + ax + b chia hết cho x2 - 3x - 4
c) 3x2 + ax + 27 chia cho x + 5 thì dư 27
d) x3 + ax + b chia cho x + 1 thi dư 7, chia cho x - 3 thì dư 5.
a: \(\Leftrightarrow2x^2+8x+\left(a-8\right)x+4\left(a-8\right)-4a+28⋮x+4\)
hay a=7
Đúng 2
Bình luận (0)
xác định hệ số a,b để:
a) 4x3+ax+b chia hết cho x-2 và x+1
b) x4+ax+b chia hết cho x2-x+1
Cảm ơn nhiều ví đã giúp em ạ
\(a,4x^3+ax+b⋮x-2\\ \Leftrightarrow4x^3+ax+b=\left(x-2\right)\cdot a\left(x\right)\)
Thay \(x=2\Leftrightarrow32+2a+b=0\Leftrightarrow2a+b=-32\left(1\right)\)
\(4x^3+ax+b⋮x+1\\ \Leftrightarrow4x^3+ax+b=\left(x+1\right)\cdot b\left(x\right)\)
Thay \(x=-1\Leftrightarrow-4-a+b=0\Leftrightarrow a-b=-4\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\) ta có hệ \(\left\{{}\begin{matrix}2a+b=-32\\a-b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a=-36\\b=a+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-12\\b=-8\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Xác định các hằng số a và b sao cho x4+ax+b chia hết cho x2-1
Đây là phương pháp đồng nhất hạng tử (cách này hơi khó hiểu vì dành cho lớp chuyên toán hoặc đội tuyển)
sau khi lấy x4+ax+b chia cho x2-1 ta được x2+1 dư ax+b+1
ta có x4+ax+b = (x2-1)(x2+cx+d)
=>x4+ax+b=x4+cx3+dx2-x2-cx-d
Tương đương bậc của 2 bên ( ko cần ghi bậc chỉ cần ghi hệ số)
x4 =x4 => 0
0x3 =cx3 => c=0
0x2=(d-1)x2 => d-1 = 0 ( lấy x2 chung)
ax=-cx => a=-c
b=-d
Từ những điều trên ta kết luận
a=0 (a=-c mà c=0)
b=1 (b=-d mà d=1)
Đúng 0
Bình luận (0)
Xác định các hằng số a và b sao cho
a) x^4 + ax + b chia hết cho x^2 - 4
b) x^4 + ax^ + bx - 1 chia hết cho x^2 - 1
c) x^3 + ax + b chia hết cho x^2 + 2x - 2
(Chia đa thức cho đa thức)

Chỉ ý kiến của mk thôi
chưa chắc đúng
Tham khảo nhé
Đúng 0
Bình luận (0)
Xác định các hằng số a và b sao cho: x^4+4 chia hết cho x^2+ax+b
1,Xác định các hằng số a,b sao cho x^3+ax+b chia hết cho x^2+x-2
Ta có :
Nghiệm của x2 + x - 2 là x = 1 và x = -2
=> Để x3 + ax + b chia hết cho x2 + x - 2
thì x3 + ax + b cũng nhận x = 1 và x = -2 làm nghiệm
+) Với x = 1
Thế vào x3 + ax + b ta được
13 + a.1 + b = 0
=> 1 + a + b = 0
=> a + b = -1 (1)
+) Với x = -2
Thế vào x3 + ax + b ta được
(-2)3 + a.(-2) + b = 0
<=> -8 - 2a + b = 0
<=> -8 = 2a - b (2)
Từ (1) và (2) => \(\hept{\begin{cases}a+b=-1\\2a-b=-8\end{cases}}\)
Lấy (1) cộng (2) theo vế => 3a = -9 => a = -3
Thế a = -3 vào (1) => -3 + b = -1 => b = 2
Vậy \(\hept{\begin{cases}a=-3\\b=2\end{cases}}\)
Hoặc là dùng cách này
Ta có : x3 + ax + b có bậc 3
x2 + x - 2 có bậc là 2
=> Thương là một đa thức bậc 1
Giả sử đa thức thương đó là x + c + d
=> x3 + ax + b chia hết cho x2 + x - 2
khi và chỉ khi x3 + ax + b = ( x2 + x - 2 )( x + c + d )
<=> x3 + ax + b = x3 + cx2 + dx2 + x2 + cx + dx - 2x - 2c - 2d
<=> x3 + ax + b = x3 + x2( c + d + 1 ) + x( c + d - 2 ) - ( 2c + 2d )
Đồng nhất hệ số ta được :
\(\hept{\begin{cases}c+d+1=0\\c+d-2=a\\2c+2d=-b\end{cases}}\Leftrightarrow\hept{\begin{cases}a=-3\\b=2\end{cases}}\)
Vậy a = -3 ; b = 2
Chử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh HiểnChử Mạnh Hiển
Xác định các hằng số a và b sao cho:
a) x^4+ax+b chia hết cho x^2-4
a ) \(x^2-4=x^2-2^2=\left(x-2\right)\left(x+2\right)\)
\(f\left(x\right)=x^4+ax+b\)
Theo định lí bơ zu
\(\Rightarrow f\left(2\right)=16+2b+b=0\)
\(\Leftrightarrow2a+b=-16\) ( 1 )
\(\Rightarrow f\left(-2\right)=16-2a+b=0\)
\(\Leftrightarrow-2a+b=-16\) ( 2 )
Từ ( 1 ) và ( 2 ) \(\Leftrightarrow a=0;b=-16\)
Đúng 0
Bình luận (1)
Bài 1: Tìm giá trị nhỏ nhất hoặc lớn nhất của các biểu thức sau:a) A a4-2a3+3a2-4a+5b) B dfrac{x^2+4x-6}{3}c) C dfrac{4+5left|1-2xright|}{7}Bài 2: a) Tìm a sao cho x4-x3+6x2-x+a chia hết cho đa thức x2-x+5.b) Xác định hằng số a và b sao cho x4+ax2+b chia hết cho x2-x+1Bài 3: Tính giá trị của biểu thức: A x17-12x14+...-12x12+12x-1 với x11
Đọc tiếp
Bài 1: Tìm giá trị nhỏ nhất hoặc lớn nhất của các biểu thức sau:
a) A= a4-2a3+3a2-4a+5
b) B= \(\dfrac{x^2+4x-6}{3}\)
c) C= \(\dfrac{4+5\left|1-2x\right|}{7}\)
Bài 2:
a) Tìm a sao cho x4-x3+6x2-x+a chia hết cho đa thức x2-x+5.
b) Xác định hằng số a và b sao cho x4+ax2+b chia hết cho x2-x+1
Bài 3: Tính giá trị của biểu thức: A= x17-12x14+...-12x12+12x-1 với x=11



















