Cho hình bình hành ABCD có tâm là O. Tìm các véctơ từ 5 điểm A, B, C, D, O
a) bằng véctơ AB; OB
b) Có độ dài bằng OB
Cho hình bình hành ABCD có tâm là O . Tìm các vectơ từ 5 điểm A B C D O a). Bằng vectơ AB ; OB. b). Có độ dài bằng OB .
Bằng \(\overrightarrow{AB}\) là \(\overrightarrow{DC}\)
Bằng \(\overrightarrow{OB}\) là \(\overrightarrow{DO}\)
Có độ dài bằng OB là \(\overrightarrow{OB};\overrightarrow{BO};\overrightarrow{OD};\overrightarrow{DO}\)
a) Bằng vectơ AB :
\(\overrightarrow{DC}\)
Bằng vectơ OB :
\(\overrightarrow{DO}\)
b)Có độ dài bằng OB :
\(\overrightarrow{OD},
\overrightarrow{DO},
\overrightarrow{BO}\)
Cho hình bình hành ABCD tâm O. Chứng minh OA+OB+OC+OD= véctơ 0
Cho hình bình hành ABCD. Trên các cạnh AB; BC; CD; DA lấy các điểm E; F; G; H sao cho AE = CG; BF = DH. CMR:
a, Xác định tâm đối xứng của hình bình hành ABCD
b, EFGH là hình bình hành và tìm tâm đối xứng
c, Gọi O là giao điểm của AC và BD, O còn là tâm đối xứng của hình bình hành nào?
Cho hình bình hành ABCD. O là giao điểm của 2 đg chéo.Trên các cạnh AB, BC, CD,DA ta lần lượt lấy các điểm E,F,G,H sao cho AE=CG, BF=DH
a, Xác định tâm đối xứng của hình bình hành ABCD
b, Chứng minh EFGH là hình bình hành, tìm tâm đối xứng của nó
c, O còn là tâm đối xứng của những hình bình hành nào ?
Cho hình bình hành ABCD. Chứng minh véctơ CD + véctơ CB = véctơ CA.
\(\overrightarrow{CD}+\overrightarrow{CB}=\overrightarrow{CD}+\overrightarrow{DA}=\overrightarrow{CA}\)
Cho hình bình hành ABCD. O là giao điểm của 2 đg chéo. Trên cac cạnh AB, BC, CD,DA ta lần lượt lấy các điểm E,F,G,H sao cho AE=CG,BF=DH
a, Xác định tâm đối xứng cưa hình bình hành ABCD
b, CM : EFGH là hình bình hành, tìm tâm đối xứng của nó
c, O còn là tâm đối xứng của hình bình hành nào?
1)Cho hình bình hành ABCD, xác định các vectơ DA+DC,AB+DA.
2)Cho 5 điểm A, B, C, D, E. Chứng minh rằng: AC-ED+CD+EC-BC = AB
3)Cho hình vuông ABCD, tâm O cạnh bằng a.
a) Xác định vecto BA+DA+AC, AB+CA+BC, AB+AC.
b) Tính độ dài vecto DA+DC, AB-BC
1: ABCD là hình bình hành
=>\(\overrightarrow{DA}+\overrightarrow{DC}=\overrightarrow{DB}\)
\(\overrightarrow{AB}+\overrightarrow{DA}=\overrightarrow{DA}+\overrightarrow{AB}=\overrightarrow{DB}\)
2: \(\overrightarrow{AC}-\overrightarrow{ED}+\overrightarrow{CD}+\overrightarrow{EC}-\overrightarrow{BC}\)
\(=\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DE}+\overrightarrow{EC}+\overrightarrow{CB}\)
\(=\overrightarrow{AD}+\overrightarrow{DE}+\overrightarrow{EC}+\overrightarrow{CB}\)
\(=\overrightarrow{AE}+\overrightarrow{EC}+\overrightarrow{CB}=\overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow{AB}\)
3:
a: \(\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AC}\)
\(=-\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{0}\)
\(\overrightarrow{AB}+\overrightarrow{CA}+\overrightarrow{BC}\)
\(=\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BC}\)
\(=\overrightarrow{CB}+\overrightarrow{BC}=\overrightarrow{0}\)
Gọi H là trung điểm của BC
Xét ΔABC có AH là đường trung tuyến
nên \(\overrightarrow{AB}+\overrightarrow{AC}=2\cdot\overrightarrow{AH}\)
b: ABCD là hình vuông
=>\(DB^2=DA^2+AB^2\)
=>\(DB^2=a^2+a^2=2a^2\)
=>\(DB=a\sqrt2\)
ABCD là hình vuông
=>\(\overrightarrow{DA}+\overrightarrow{DC}=\overrightarrow{DB}\)
=>\(\left|\overrightarrow{DA}+\overrightarrow{DC}\right|=DB=a\sqrt2\)
\(\overrightarrow{AB}-\overrightarrow{CB}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\)
=>\(\left|\overrightarrow{AB}-\overrightarrow{CB}\right|=CA=a\sqrt2\)
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD
A. 
B. 
C. 
D. 
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A (1;1;0), B (0;-1;2). Biết rằng có hai mặt phẳng cùng đi qua hai điểm A, O và cùng cách B một khoảng bằng √3. Véctơ nào trong các véctơ dưới đây là một véctơ pháp tuyến của một trong hai mặt phẳng đó.
![]()
![]()
![]()
![]()
Chọn C
Phương trình đường thẳng qua hai điểm A, O có dạng 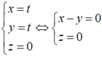
Gọi (P) là mặt phẳng cùng đi qua hai điểm A, O nên (P) : m (x-y)+nz=0, m²+n² > 0. Khi đó véctơ pháp tuyến của (P) có dạng ![]()
![]()
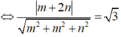
![]()
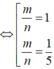
Vậy một véctơ pháp tuyến của một trong hai mặt phẳng đó là 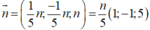
GIÚP EM VỚI Ạ, CHIỀU NAY EM THI RỒI :(
Câu 5: Trong mặt phẳng toạ độ Oxy cho A(3;-1) ; B(-1;2) ; và I(1;1). Xác định toạ độ điểm C, D sao cho tứ giác ABCD là hình bình hành biết I là trong tâm tam giác ABC. Tìm toạ tâm O của hình bình hành ABCD
I là trọng tâm của ΔABC
=>\(\left\{{}\begin{matrix}x_A+x_B+x_C=3\cdot x_I\\y_A+y_B+y_C=3\cdot y_I\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3+\left(-1\right)+x_C=3\cdot1=3\\-1+2+y_C=3\cdot1=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_C=3-2=1\\y_C=3-1=2\end{matrix}\right.\)
Vậy: C(1;2)
Ta có: A(3;-1); B(-1;2); C(1;2); D(x;y)
=>\(\overrightarrow{AB}=\left(-4;3\right);\overrightarrow{DC}=\left(1-x;2-y\right)\)
ABCD là hình bình hành
=>\(\overrightarrow{AB}=\overrightarrow{DC}\)
=>\(\left\{{}\begin{matrix}1-x=-4\\2-y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\)
Vậy: D(5;-1)
Tâm O của hình bình hành ABCD sẽ là trung điểm của AC
A(3;-1); C(1;2); O(x;y)
=>\(\left\{{}\begin{matrix}x=\dfrac{3+1}{2}=\dfrac{4}{2}=2\\y=\dfrac{-1+2}{2}=\dfrac{1}{2}\end{matrix}\right.\)
Áp dụng công thức trọng tâm:
\(\left\{{}\begin{matrix}x_A+x_B+x_C=3x_I\\y_A+y_B+y_C=3y_I\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_C=3x_I-\left(x_A+x_B\right)=1\\y_C=3y_I-\left(y_A+y_B\right)=2\end{matrix}\right.\)
\(\Rightarrow C\left(1;2\right)\)
Đặt tọa độ D là \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-4;3\right)\\\overrightarrow{DC}=\left(1-x;2-y\right)\end{matrix}\right.\)
ABCD là hình bình hành \(\Leftrightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow\left\{{}\begin{matrix}1-x=-4\\2-y=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\) \(\Rightarrow D\left(5;-1\right)\)
Tâm O hình bình hành là trung điểm đường chéo AC nên áp dụng công thức trung điểm:
\(\left\{{}\begin{matrix}x_O=\dfrac{x_A+x_C}{2}=2\\y_O=\dfrac{y_A+y_C}{2}=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow O\left(2;\dfrac{1}{2}\right)\)