Chọn C
Phương trình đường thẳng qua hai điểm A, O có dạng 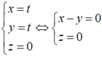
Gọi (P) là mặt phẳng cùng đi qua hai điểm A, O nên (P) : m (x-y)+nz=0, m²+n² > 0. Khi đó véctơ pháp tuyến của (P) có dạng ![]()
![]()
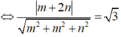
![]()
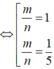
Vậy một véctơ pháp tuyến của một trong hai mặt phẳng đó là 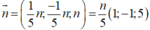
Chọn C
Phương trình đường thẳng qua hai điểm A, O có dạng 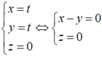
Gọi (P) là mặt phẳng cùng đi qua hai điểm A, O nên (P) : m (x-y)+nz=0, m²+n² > 0. Khi đó véctơ pháp tuyến của (P) có dạng ![]()
![]()
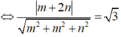
![]()
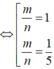
Vậy một véctơ pháp tuyến của một trong hai mặt phẳng đó là 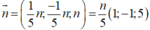
Trong không gian với hệ trục Oxyz, cho hai điểm M (0;-1;2), N (-1; 1; 3). Một mặt phẳng (P) đi qua M, N sao cho khoảng cách từ điểm K (0;0;2) đến mặt phẳng (P) đạt giá trị nhỏ nhất. Tìm tọa độ véctơ pháp tuyến của mặt phẳng (P).
A . n → = 1 ; - 1 ; 1
B . n → = 1 ; 1 ; - 1
C . n → = 2 ; - 1 ; 1
D . n → = 2 ; 1 ; - 1
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;2;3), B(-2,1,5). Véctơ nào dưới đây là véctơ pháp tuyến của mặt phẳng (OAB).
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(0;-1;2) và N(-1;1;3). Một mặt phẳng (P) đi qua M, N sao cho khoảng cách từ điểm K(0;0;2) đến mặt phẳng (P) đạt giá trị lớn nhất. Tìm tọa độ véctơ pháp tuyến n → của mặt phẳng
A. n → =(1;-1;1)
B. n → =(1;1;-1)
C. n → =(2;-1;1)
D. n → =(2;1;-1)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 x - z + 1 = 0 . Tọa độ một véctơ pháp tuyến của mặt phẳng (P) là:
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho các điểmA(6;0;0), B(0;3;0) và mặt phẳng (P): x-2y+2z=0. Gọi d là đường thẳng đi qua M(2;2;0), song song với (P) và tổng khoảng cách từ A,B đến đường thẳng d đạt giá trị nhỏ nhất. Véctơ nào dưới đây là một véctơ chỉ phương của d?
![]()
![]()
![]()
![]()
Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (P) đi qua gốc toạ độ và nhận ![]() =(3;2;1) là véctơ pháp tuyến. Phương trình của mặt phẳng (P) là:
=(3;2;1) là véctơ pháp tuyến. Phương trình của mặt phẳng (P) là:
A. 3x+2y+z-14=0
B. 3x+2y+z=0
C. 3x+2y+z+2=0
D. x+2y+3z=0.
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d 1 : x - 1 2 = y - 2 - 2 = z + 1 - 1 và
d 2 : x = t y = 0 z = - t . Mặt phẳng (P) qua d 1 và tạo với d 2 một góc 45 o và nhận véctơ n ⇀ ( 1 ; b ; c ) làm véc tơ pháp tuyến. xác định tích bc.
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho hai điểm A(1;1;0), B(2;-1;1). Một vectơ pháp tuyến n → của mặt phẳng (OAB) (Với O là gốc tọa độ) là
A. (-3;1;-1)
B. (1;-1;-3)
C. (1;-1;3)
D. (1;1;3)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A ( 1 ; - 1 ; 2 ) và B ( 2 ; 1 ; - 4 ) . Véctơ A B → có tọa độ là
![]()
![]()
![]()
![]()