Cho tam giác ABC, trên tia BA lấy D, trên tia đối tia CA lấy E sao cho BD=CE. qua D kẻ đường thẳng song song AC cắt BC tại F. Gọi I là giao điểm của DE và BC. Biết ID=IE. Chứng minh tam giác AbC cân

Những câu hỏi liên quan
Cho tam giác ABC cân A. Trên cạnh AB lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD=CE. Gọi I là giao điểm của DE và BC. Qua E vẽ đường thẳng song song với AB, cắt BC tại F
a/ chứng minh: tam giác BDI= tam giác FEI
b/ chứng minh: I là trung điểm của DE
Giúp mik với, sáng mai phải nộp cô rồi😄
( vẽ hình nữa nhé😙 )
Xem chi tiết
CHO TAM GIÁC ABC CÂN TẠI A. TRÊN AB LẤY D . TRÊN TIA ĐỐI AC LẤY E SAO CHO BD=CE. ĐƯỜNG THẲNG QUA D SONG SONG AC CẮT BC TẠI F . GỌI I LÀ GIAO ĐIỂM CỦA DE VÀ BC . CHỨNG MINH A, TAM GIÁC FBD CÂN
B, I LÀ TRUNG ĐIỂM DE
C, AD+AE KHÔNG ĐỔI KHI D, E THAY ĐỔI
Bài này đáng lẽ phải là TRÊN TIA ĐỐI CA LẤY E SAO CHO BD=CE. Quên vẽ điểm F mà câu a) dễ nên tự thêm vô nha.

a) Ta có ^BFD = ^ACB ( DF // AC, đồng vị)
Mà ^ABC = ^ACB ( tam giác ABC cân tại A)
=> ^ABC = ^BFD
Vậy tam giác FBD cân tại D (đpcm)
b) Kẻ \(DM\perp BC;EN\perp BC\)
Ta thấy ngay: \(\Delta BDM=\Delta CEN\left(ch-gn\right)\)
=> MD = NE (hai cạnh tương ứng)
=> \(\Delta DMI=\Delta ENI\left(g.c.g\right)\)
=> DI = EI hay I là trung điểm của DE (đpcm)
c) Ta có: AD + AE = AB - BD + AC + CE = AB + AC = 2AB (không đổi)
=> đpcm...
Đề bị sai em kiểm tra lại đề đi! Chỗ trên AB lấy D , trên tia đối AC lấy E sao cho BD = CE ấy.
đề đúng nha chị D thuộc AB, E thuộc AC
Xem thêm câu trả lời
Cho tam giác ABC cân tại A. Trên cạnh AB lấy D , trên tia đối của CA lấy điểm E sao cho BD= CE. Qua D kẻ đường thẳng song song với AC cắt BC tại F. Gọi O là giao điểm của DE và CF. Chứng minh
a) Tam giác BDF cân
b) O là trung điểm CF
c) CD // EF
Cho tam giác ABC, trên tia BA lấy D, trên tia đối tia CA lấy E sao cho BD=CE. Qua D kẻ đường thẳng song song AC cắt BC tại F.Gọi I là giao điểm của DE và BC. biết ID=IE. Chứng minh tam giác ABC cân.
Xét 2 \(\Delta IDF\) và \(\Delta IEC\) có:
\(\widehat{DIF}\)\(=\widehat{CIE}\) (2 góc đối đỉnh)
\(ID=IE\left(gt\right)\)
DF//AC (gt)
\(\Rightarrow\)\(\widehat{IDF}\)\(=\widehat{CEI}\) (2 góc so le trong)
\(\Rightarrow\Delta IDF=\Delta IEC\left(g.c.g\right)\)
\(\Rightarrow DF=CE\)
mà CE=BD (gt)
\(\Rightarrow DF=BD\)
\(\Rightarrow\Delta BDF\) cân tại D
\(\Rightarrow\)\(\widehat{B}=\widehat{DFB}\) (1)
Ta có: DF//AC (gt)
\(\Rightarrow\)\(\widehat{ACB}=\widehat{DFB}\) (2 góc đồng vị) (2)
Từ (1) và (2) \(\Rightarrow\)\(\widehat{B}=\widehat{ACB}\)
\(\Rightarrow\Delta ABC\) cân tại A
Chúc bạn học tốt nha!!!!
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D. Qua D kẻ đường thẳng song song với AC cắt BC tại E. Trên tia đối của tia CA lấy điểm F sao cho CF= BD. Gọi I là trung điểm của EC. Chứng minh D, I, F thẳng hàng.
Xét ΔABC có
DE//AC
nên \(\dfrac{DE}{AC}=\dfrac{BD}{AB}\)
hay DE=BD
mà BD=CF
nên DE=CF
Xét tứ giác DEFC có
DE//CF
DE=CF
Do đó: DEFC là hình bình hành
Suy ra: Hai đường chéo DF và EC cắt nhau tại trung điểm của mỗi đường
mà I là trung điểm của EC
nên I là trung điểm của DF
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD=CE. Gọi M là giao điểm của DE và BC. Qua E vẽ đường thẳng song song với AB, cắt BC tại F. Chứng minh: a) tam giác BDM= tam giác FEM. b) M là trug điểm của DE
Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Gọi I là giao điểm của DE và BC. Qua E vẽ đường thẳng song song với AB, cắt BC tại F.
a) Chứng minh: tam giác BDI = tam giác FEI.
b) Chứng minh I là trung điểm của DE.
Cho tam giác ABC cân tại A. Trên Tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Gọi I là giao điểm của BE và CD. Chứng minh rằng BC song song DE.
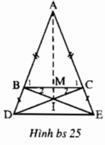
Các tam giác cân ABC và ADC có chung góc ở đỉnh ∠A nên ∠B1 = ∠ADE. Mà hai góc này ở vị trí đồng vị nên suy ra BC // DE.
Đúng 1
Bình luận (0)
Cho tam giác ABC, trên tia đối của BC lấy điểm D, trên tia đối của CD lấy điểm E sao cho BD=BC=CE. Qua D kẻ đường thẳng song song với AB cắt AC taih H. Qua E kẻ dường thẳng song song với AC cắt AB tại K. Chúng giao nhau tại I. a. Tứ giác PHAC là hình gì? Vì sao? b. Tia IA cát BC tại M. Chứng minh MB=MC. c. Tìm điều kiện của tam giác ABC để DHKE là hình thang cân.
















