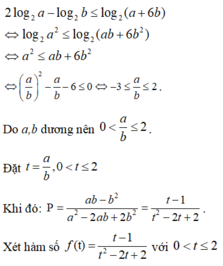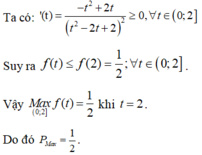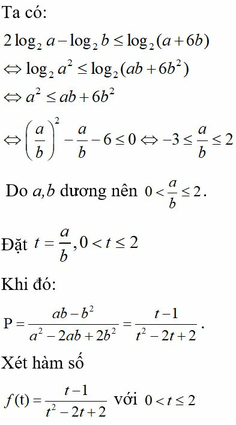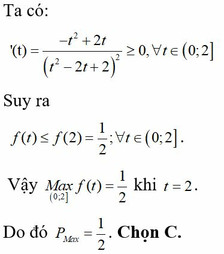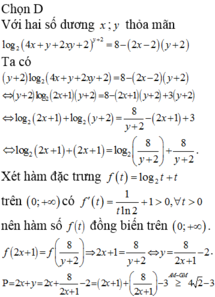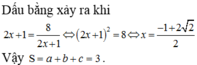Cho a,b là các số nguyên dương thỏa mãn: log2(log2a(log2b21000)) = 0. Tính giá trị lớn nhất của ab

Những câu hỏi liên quan
Cho hai số thực dương a, b thỏa mãn hệ thức:
2
log
2
a
-
log
2
b
≤
log
2
a
+
6
b
. Tìm giá trị lớn nhất
P
m
a
x...
Đọc tiếp
Cho hai số thực dương a, b thỏa mãn hệ thức: 2 log 2 a - log 2 b ≤ log 2 a + 6 b . Tìm giá trị lớn nhất P m a x của biểu thức P = a b - b 2 a 2 - a b + 2 b 2
![]()
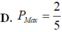
Cho hai số thực dương a, b thỏa mãn hệ thức:
2
log
2
a
-
log
2
b
≤
log
2
a
+
6
b
. Tìm giá trị lớn nhất
P
m
a
x
của biểu thức
P...
Đọc tiếp
Cho hai số thực dương a, b thỏa mãn hệ thức: 2 log 2 a - log 2 b ≤ log 2 a + 6 b . Tìm giá trị lớn nhất P m a x của biểu thức P = a b - b 2 a 2 - 2 a b + 2 b 2
A. 1
B. 0
C. 1 2
D. - 1 2
Cho hai số thực dương a; b thỏa mãn log2(a + 1) + log2(b + 1) ≥ 6 Giá trị nhỏ nhất của biểu thức S = a + b là
A.12
B.14
C. 8
D.16
Chọn B.
Ta có 6 ≤ log2(a + 1) + log2(b + 1) = log2[(a + 1)(b + 1) ]
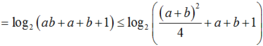
Suy ra: ![]() hay ( a + b) 2 + 4( a + b) + 4 ≥ 256
hay ( a + b) 2 + 4( a + b) + 4 ≥ 256
Tương đương: (a + b) 2 + 4(a + b) - 252 ≥ 0
Suy ra: a + b ≥ 14
Đúng 0
Bình luận (0)
Cho các số a, b, c nguyên dương thỏa mãn ab+bc = 518 và bc-ac = 360. Tính giá trị lớn nhất của tích abc.
Cho các số thực a,b1 thỏa mãn điều kiện
log
2
a
+
log
3
b
1
. Tìm giá trị lớn nhất của biểu thức
P
log
3
a
+
log
2
b
Đọc tiếp
Cho các số thực a,b>1 thỏa mãn điều kiện log 2 a + log 3 b = 1 . Tìm giá trị lớn nhất của biểu thức P = log 3 a + log 2 b
![]()
![]()
![]()
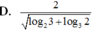
Cho các số thực a,b 1 thỏa mãn điều kiện
l
o
g
2
a
+
log
3
b
1
.Tìm giá trị lớn nhất của biểu thức
P
l
o
g
3
a
+
log
2
b
A.
l
o...
Đọc tiếp
Cho các số thực a,b > 1 thỏa mãn điều kiện l o g 2 a + log 3 b = 1 .
Tìm giá trị lớn nhất của biểu thức P = l o g 3 a + log 2 b
A. l o g 2 3 + log 3 2
B. l o g 3 2 + log 2 3
C. 1 2 l o g 2 3 + log 3 2
D. 2 l o g 2 3 + log 3 2
Cho các số a,b0 thỏa mãn
log
3
a
log
6
log
2
a
+
b
. Giá trị của bằng A. 18 B. 45 C. 27 D. 36
Đọc tiếp
Cho các số a,b>0 thỏa mãn
log
3
a
=
log
6
=
log
2
a
+
b
. Giá trị của ![]() bằng
bằng
A. 18
B. 45
C. 27
D. 36
Cho hai số dương x, y thỏa mãn
l
o
g
2
(
4
x
+
y
+
2
x
y
+
2
)
y
+
2
8
-
2
x
-
2
y
+
2...
Đọc tiếp
Cho hai số dương x, y thỏa mãn l o g 2 ( 4 x + y + 2 x y + 2 ) y + 2 = 8 - 2 x - 2 y + 2 . Giá trị nhỏ nhất của P = 2 x + y là số có dạng M = a b + c với a , b ∈ ℕ , a > 2 . Tính S = a + b + c
A. 17
B. 7
C. 19
D. 3
Trong không gian Oxyz, cho các điểm A(2t;2t;0), B(0;0;t) với t 0 Cho điểm P di động thỏa mãn
O
P
→
.
A
P
→
+
O
P
→
.
B
P
→
+
A
P
→...
Đọc tiếp
Trong không gian Oxyz, cho các điểm A(2t;2t;0), B(0;0;t) với t >0 Cho điểm P di động thỏa mãn O P → . A P → + O P → . B P → + A P → . B P → = 3 . Biết rằng có giá trị t = a b với a,b nguyên dương và a b tối giản sao cho OP đạt giá trị lớn nhất là 3. Tính giá trị Q=2a+b?
A. 5
B. 13
C. 11
D. 9