cho tam giác ABC có 3 góc nhọn . đường cao AK và BH cắt nhau tại I . chứng minh rằng tan góc B x tan góc C = \(\dfrac{AK}{IK}\)

Những câu hỏi liên quan
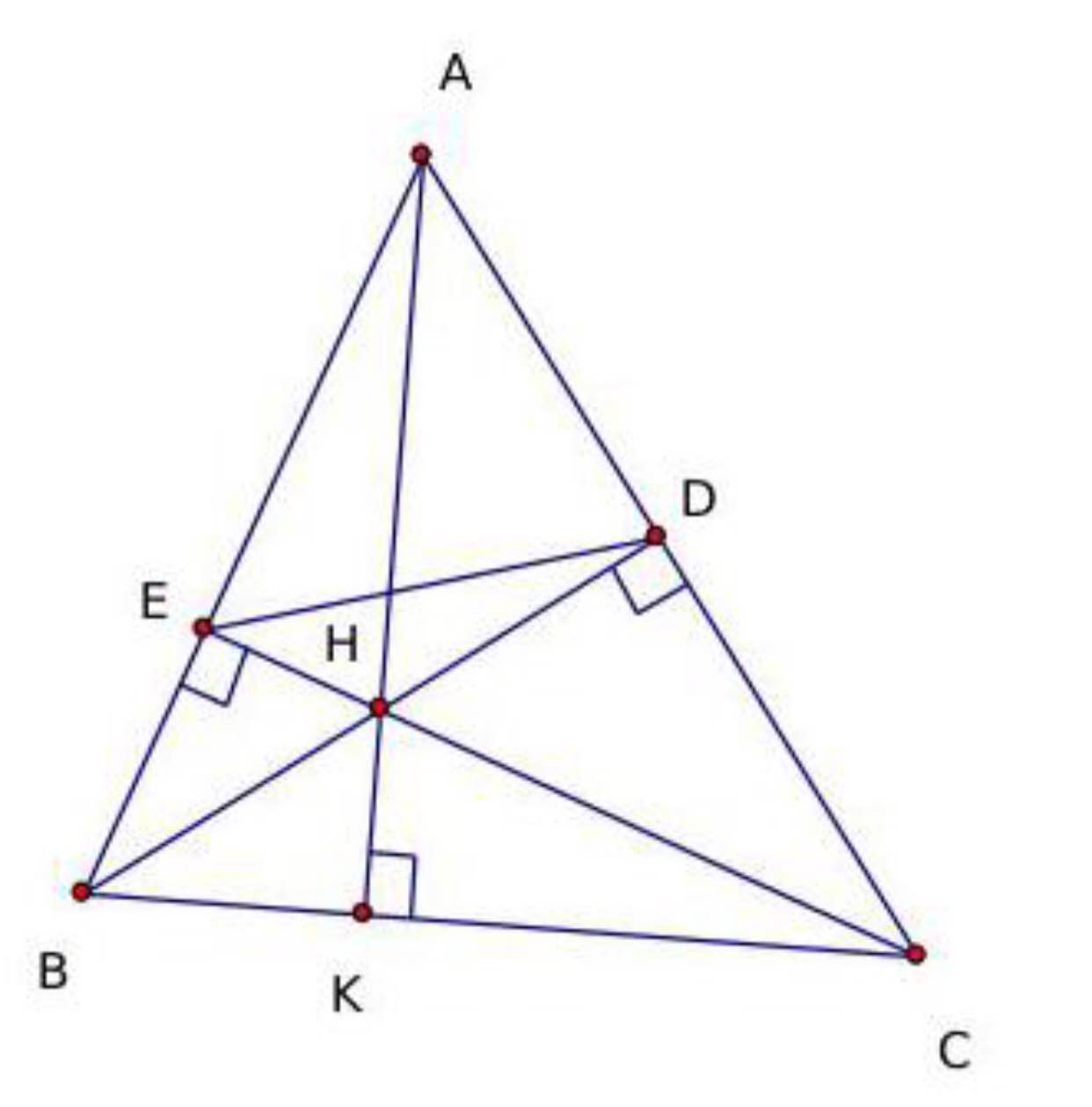
Cho tam giác ABC nhọn, các đường cao AK, BD, CE cắt nhau tại H.
1. Chứng minh: \(\dfrac{KC}{KB}=\dfrac{AC^2+CB^2-BA^2}{CB^2+BA^2-AC^2}\)
2.Giả sử: \(HK=\dfrac{1}{3}AK.\) Chứng minh rằng: tan B . tan C = 3
a, Áp dụng định lí Pitago
\(\dfrac{AC^2+CB^2-BA^2}{CB^2+BA^2-AC^2}\\ =\dfrac{AK^2+KC^2+\left(BK+KC\right)^2-AB^2}{\left(BK+KC^2\right)+BA^2-\left(AK+KC\right)^2}\\ =\dfrac{2CK^2+2BK.CK}{2BK^2+2BK.Ck}\\ =\dfrac{2CK\left(CK+BK\right)}{2BK\left(BK+CK\right)}=\dfrac{CK}{BK}\)
b, Ta có
\(tanB=\dfrac{AK}{BK};tanC=\dfrac{AK}{CK}\\ Nên:tanBtanC=\dfrac{AK^2}{BK.CK}\left(1\right)\\ Mặt.khác.ta.có:\\ B=HKC\\ mà:tanHKc=\dfrac{KC}{KH}\\ Nên.tanB=\dfrac{KC}{KH}\\ Tương.tự.tanC=\dfrac{KB}{KH}\\ \Rightarrow tanB.tanC=\dfrac{KB.KC}{KH^2}\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow\left(tanB.tanC\right)^2=\left(\dfrac{AK}{KH}\right)^2\\ Theo.GT:\\ HK=\dfrac{1}{3}AK\Rightarrow tanB.tanC=3\)
c, Chứng minh được
\(\Delta ABC.và.\Delta ADE.đồng.dạng\\ \Rightarrow\dfrac{S_{ABC}}{S_{ADE}}=\left(\dfrac{AB}{AD}\right)^2\left(3\right)\)
Mà
\(\widehat{BAC}=60^0\Rightarrow\widehat{ABD}=30^0\\\Rightarrow AB=2AD\left(4\right)\\ Từ.\left(3\right)và\left(4\right)=4\\ \Rightarrow S_{ADE}=30cm^2\)
Đúng 1
Bình luận (0)
Cho tam giác ABC cân góc A nhọn Đường cao BH giao AK tại I
a, chứng minh góc ABC nhọn
b,vẽ BX vuông góc với AB ,Bx cắt tia đối của tia CA tại D chứng minh BC là phân giác của góc HBD
c, vẽ CN vuông góc với CD chứng minh HN song song với AK
cho tam giác ABC có 3 góc nhọn (AB>AC)nội tiếp đường tròn (O;R) Hai đường cao AD và BE cắt nhau tại H 1, chúng minh tứ giác CEHD 2,kẻ đường kính AK của (O). chứng minh AC.AB= AK.AD 3, kẻ KI vuông góc với BC (I thuộc BC ) chứng minh : a,AB/BK=IC/IK b,AC/CK+AB/BK = BC /IK
1:Xét tứ giác CEHD có
góc CEH+góc CDH=180 độ
=>CEHD là tứ giác nội tiếp
2 Xét (O) có
ΔAKC nội tiếp
AK là đường kính
=>ΔACK vuông tại C
Xét ΔACK vuông tại C và ΔADB vuông tại D có
góc AKC=góc ABD
=>ΔACK đồng dạng với ΔADB
=>AC/AD=AK/AB
=>AB*AC=AK*AD
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A ( AB<AC) có đường cao AH. Gọi M là trung điểm của AC, BM cắt AH tại I. vẽ AK vuông góc với BM tại K,
a) chứng minh : tam giác BHI đồng dạng với tam giác AKI và IB. IK = IA.IH
b) chứng minh: góc BAH = góc BKH
c) tia AK cắt BC tại D. Chứng minh: HD.KC = HK.DC
a: Xét ΔBHI vuông tại H và ΔAKI vuông tại K có
góc BIH=góc AIK
=>ΔBHI đồng dạng vói ΔAKI
=>IB*IK=IA*IH
b: góc BHA=góc BKA=90 độ
=>BHKA nội tiếp
=>góc BAH=góc BKH
Đúng 1
Bình luận (1)
Cho tam giác ABC có 3 góc nhọn. Qua A vẽ đường thẳng vuông góc với AB. Đường thẳng này cắt tia phân giác góc ABC tại M. Kẻ MH vuông góc với BC(H thuộc BC)
a) Chứng minh tam giác ABM = tam giác HBM
b) Kẻ đường cao Ak của tam giác ABC. Chứng minh AK // HM
c) Gọi N là giao điểm của BM và AK. Chứng minh HN // AM
Bài 3: Cho tam giác ABC vuông tại A. Đường phân giác BH. Kẻ HK vuông góc với BC tại K. a) Chứng minh ABC = KHC b) Chứng minh BH là đường trung trực của AK. c) Ké CD vuông góc với BH tại D, hai đường thẳng BA và CD cắt nhau tại I. Chứng minh I,H.K thắng hàng. d) Tìm điều kiện của AABC để AADK là tam giác đều.
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Hai đường cao AK và CI của tam
giác ABC cắt nhau tại H (K ∊ BC, I ∊ AB).
a) Chứng minh: Tứ giác BIHK nội tiếp được một đường tròn.
b) Đường thẳng AK cắt đường tròn tại D (D khác A). Kẻ đường kính AF. Đường thẳng qua O và vuông góc với BC cắt đường tròn (O) tại E (E thuộc cung nhỏ DF). Chứng minh: AE là tia phân giác của góc DAF
Đọc tiếp
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Hai đường cao AK và CI của tam giác ABC cắt nhau tại H (K ∊ BC, I ∊ AB). a) Chứng minh: Tứ giác BIHK nội tiếp được một đường tròn. b) Đường thẳng AK cắt đường tròn tại D (D khác A). Kẻ đường kính AF. Đường thẳng qua O và vuông góc với BC cắt đường tròn (O) tại E (E thuộc cung nhỏ DF). Chứng minh: AE là tia phân giác của góc DAF
a: góc BIH+góc BKH=180 độ
=>BIHK nội tiếp
b: OE vuông góc BC
=>sđ cung EB=sđ cung EC
=>góc BAE=góc CAE
Xét ΔAKB vuông tại K và ΔACF vuông tại C có
góc ABK=góc AFC
=>ΔAKB đồng dạng với ΔACF
=>góc BAK=góc CAF
=>góc DAE=góc FAE
=>AE là phân giác của góc DAF
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn. Các đường cao AK,BD,CE cắt nhau tại H.
1.Chứng minh: \(\dfrac{KC}{KB}=\dfrac{AC^2+CB^2-BA^2}{CB^2+BA^2-AC^2}\)
2. Giả sử: \(HK=\dfrac{1}{3}AK\) . Chứng minh rằng: tanB . tan C =3
3.Giả sử \(S_{ABC}=120cm^2\) và BAC = \(60^o\) . Hãy tính diện tích tam giác ADE?
Cho tam giác ABC vuông tại A. Đường phân giác BH. Kẻ HK vuông góc với BC tại K. a) Chứng minh gócABC = góc KHC b) Chứng minh BH là đường trung trực của AK. c) Kẻ CD vuông góc với BH tại D, hai đường thẳng BA và CD cắt nhau tại I. Chứng minh I,H,K thẳng hàng.