cho hình bs 4 ( hai đường thẳng a và b song song với nhau ) . cho biết số đo của mỗi góc : D1 ,D2 D3, D4

Những câu hỏi liên quan
Cho hình bs 4 (hai đường thẳng a và b song song với nhau). Cho biết số đo của mỗi góc: ∠(D1 ) ; ∠(D2 ) ; ∠(D3 ) ; ∠(D3và giải thích cách tìm.
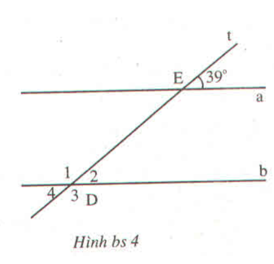
∠D2 = 39° vì là góc đồng vị với ∠E = 39°.
∠D4 = 39° vì là góc đối đỉnh với ∠D2.
∠D3 = 141° vì bù với góc ∠D4.
∠D1 = 141° vì là góc đối đỉnh với ∠D3.
Đúng 1
Bình luận (0)
Cho hình bs 4 (hai đường thẳng a và b song song với nhau). Cho biết số đo của mỗi góc: ∠(D1 ) ; ∠(D2 ) ; ∠(D3 ) ; ∠(D3và giải thích cách tìm.
Đọc tiếp
Cho hình bs 4 (hai đường thẳng a và b song song với nhau). Cho biết số đo của mỗi góc: ∠(D1 ) ; ∠(D2 ) ; ∠(D3 ) ; ∠(D3và giải thích cách tìm.
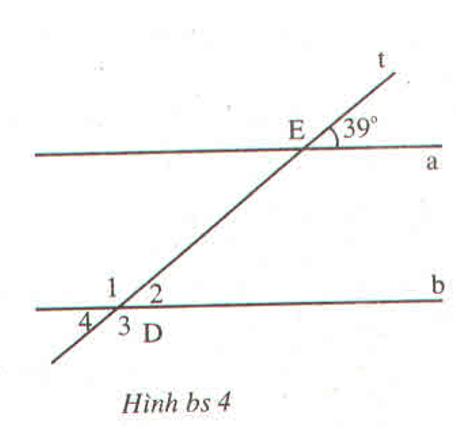
∠D2 = 39° vì là góc đồng vị với ∠E
∠D4 = 39° vì là góc đối đỉnh với ∠D2
∠D3 = 141° vì bù với góc ∠D4
∠D1 = 141° vì là góc đối đỉnh với ∠D3
Đúng 1
Bình luận (0)
Cho ba đường thẳng
d
1
:
y
2
x
-
3
;
d
2
:
y
-
x
+
3
;
d
3
:
y
-
2
x
+
1
. Lập phương trình đường thẳng
d
4
song song với
d...
Đọc tiếp
Cho ba đường thẳng d 1 : y = 2 x - 3 ; d 2 : y = - x + 3 ; d 3 : y = - 2 x + 1 . Lập phương trình đường thẳng d 4 song song với d 1 và ba đường thẳng d 2 , d 3 , d 4 đồng quy.
A. y = 2 x - 7
B. y = 2 x + 9
C. y = - 2 x + 9
D. y = - x + 9
Giao điểm A(x; y) của hai đường thẳng d 2 và d 3 là nghiệm hệ phương trình: y = - x + 3 y = - 2 x + 1 ⇔ x = - 2 y = 5 ⇒ A ( - 2 ; 5 )
Do đường thẳng d 4 // d 1 nên d 4 có dạng: y = 2x + b
Ba đường thẳng d 2 ; d 3 ; d 4 đồng quy nên điểm A(-2; 5) thuộc đường thẳng d 4 .
Suy ra: 5 = 2.(-2) + b ⇔ b = 9
Vậy phương trình đường thẳng ( d 4 ) là y = 2x + 9.
Đúng 0
Bình luận (0)
1/Cho hai đường thẳng (d1):y = x + 4 và (d2):y = - 2x - 2 a) Vẽ đồ thị (d1) và (d2) trên cùng một mặt phẳng tọa độ. b) Cho đường thẳng (d3): y = ax + b . Xác định a và b biết đường thẳng (d3) song song với đường thẳng (d1) và (d3) cắt (d2)tại điểm A có hoành độ là -3.
\(b,\left(d_3\right)\text{//}\left(d_1\right)\Leftrightarrow\left\{{}\begin{matrix}a=1\\b\ne4\end{matrix}\right.\Leftrightarrow\left(d_3\right):y=x+b\)
PT hoành độ giao điểm \(\left(d_2\right);\left(d_3\right)\) là \(x+b=-2x-2\)
Mà 2 đt cắt tại hoành độ \(-3\) nên \(x=-3\)
\(\Leftrightarrow b-3=4\Leftrightarrow b=7\)
Vậy \(\left(d_3\right):y=x+7\)
Đúng 1
Bình luận (0)
Cho các đường thẳng d1: x+y-1=0 ; d3: y=3-2x d2: y=-2x+1 ; d4: 2y=x+4 a, Hãy chỉ ra các cặp đường thẳng song song, các cặp đường thẳng cắt nhau. b, Vẽ các đường d1, d2, d3 trên cùng 1 hệ trục toạ độ.
Ta có :
+) d1 : x+y-1=0 <=> y= -x+1
+) d2 : y= -2x+1
+) d3 : y= -2x+3
+) d4 : 2y=x+4 <=> y= \(\dfrac{1}{2}\)x + 2
Suy ra :
- Cặp đường thẳng // là : d2 và d3
-Các cặp đường thẳng cắt nhau là : d1 và d2 , d1 và d3 , d1 và d4 , d2 và d4 , d3 và d4
Đúng 1
Bình luận (0)
Cho bốn đường thẳng:
d
1
:
y
x
3
+
1
;
d
2
:
y
3
3
x
-
1
;
d
3
:
y
-
x
3
+...
Đọc tiếp
Cho bốn đường thẳng:
d 1 : y = x 3 + 1 ; d 2 : y = 3 3 x - 1 ; d 3 : y = - x 3 + 1 ; d 4 : y = 3 x + 2
a. Cặp đường thẳng song song với nhau là:
A. d 1 v à d 2
B. d 2 v à d 3
C. d 1 v à d 3
D. d 2 v à d 4
Đường thẳng d 2 được viết lại thành: d 2 : y = 3 3 x - 1 = 3 x - 1
Cặp đường thẳng song song khi chúng có cùng hệ số góc và có tung độ gốc khác nhau.
Hai đường thẳng d 1 và d 2 có cùng hệ số góc là 3 và có tung độ góc khác nhau ( 1 ≠ - 1 ) nên hai đường thẳng này song song với nhau.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho hai đường thẳng (d1): y -1/3x và (d2): y 3x-2.1)Vẽ (d1) và (d2) trên cùng hệ trục.2) Bằng phép tính tìm tọa độ giao điểm của (d1) và (d2).3) Cho đường thẳng (d3): yax+b. Xác định a và b biết (d3) song song với (d2) và cắt (d1) tại điểm có hoành độ bằng 2.Giup minh voi a!
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho hai đường thẳng (d1): y = -1/3x và (d2): y = 3x-2.
1)Vẽ (d1) và (d2) trên cùng hệ trục.
2) Bằng phép tính tìm tọa độ giao điểm của (d1) và (d2).
3) Cho đường thẳng (d3): y=ax+b. Xác định a và b biết (d3) song song với (d2) và cắt (d1) tại điểm có hoành độ bằng 2.Giup minh voi a!
Cho hàm số y2x+4 có đồ thị là (d1) và hàm số y-x+1 có đồ thị là (d2)a. Vẽ (d1) và (d2) trên cùng một mặt phẳng toạ độ Oxyb. Xác định các hệ số a, b của đường thẳng yax+b (d3). Biết (d3) song song với (d1) và (d3) cắt (d2) tại một điểm có hoành độ bằng 2
Đọc tiếp
Cho hàm số \(y=2x+4\) có đồ thị là (d1) và hàm số \(y=-x+1\) có đồ thị là (d2)
a. Vẽ (d1) và (d2) trên cùng một mặt phẳng toạ độ Oxy
b. Xác định các hệ số a, b của đường thẳng \(y=ax+b\) (d3). Biết (d3) song song với (d1) và (d3) cắt (d2) tại một điểm có hoành độ bằng 2
Trong mặt phẳng tọa đô Oxy cho đường thẳng d1 y=x và d2 y=-2x+4
a. Vẽ d1 và d2
b. Cho đưởng thẳng d3 y=ã+b xác dịnh a b biết d3 song song với d1 và cắt trục hoành tại hoành độ bằng 2














