Cho tam giác ABC = tam giác A'B'C'. Biết BC = 10 cm , AB : AC = 4:3 và AB + AC bằng 14 cm .Tính các canh của tam giác A'B'C'

Những câu hỏi liên quan
Cho tam giác ABC = tam giác A'B'C'. Biết BC = 10 cm , AB : AC = 4:3 và AB + AC bằng 14 cm .Tính các canh của tam giác A'B'C'
Ta có:
AB:AC=4:3 =>\(\frac{AB}{4}=\frac{AC}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{AB}{4}=\frac{AC}{3}=\frac{AB+AC}{4+3}=\frac{14}{7}=2\)
=>\(\frac{AB}{4}=2\)=>AB=8
\(\frac{AC}{3}=2\)=>AC=4
Vì tam giác ABC= tam giác A'B'C'
=>AB=A'B' ; AC=A'C' ; BC=B'C'
Mà AB=8 ;AC=4 ;BC=10
=>A'B'=8 ;A'C'=4 ;B'C'=10
Đúng 0
Bình luận (0)
Tam giác \(ABC\) có độ dài \(AB = 4cm,AC = 6cm,BC = 9cm.\)Tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\) và có chu vi bằng 66,5 cm. Hãy tính độ dài các cạnh của tam giác \(A'B'C'\).
Vì tam giác \(ABC\) đồng dạng với tam giác \(A'B'C'\) nên tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Do đó, \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6}\). Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6} = \frac{{A'B' + B'C' + A'C'}}{{4 + 6 + 9}} = \frac{{66,5}}{{19}} = 3,5\)
Ta có:
\(\left\{ \begin{array}{l}\frac{{A'B'}}{4} = 3,5 \Rightarrow A'B' = 3,5.4 = 14\\\frac{{A'C'}}{6} = 3,5 \Rightarrow A'C' = 3,5.6 = 21\\\frac{{B'C'}}{9} = 3,5 \Rightarrow B'C' = 3,5.9 = 31,5\end{array} \right.\)
Vậy \(A'B' = 14cm,A'C' = 21cm,B'C' = 31,5cm\).
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 16,2 cm, BC = 24,3 cm; AC = 32,7 cm. Tính độ dài các cạnh của tam giác A'B'C', biết rằng A'B'C' đồng dạng với tam giác ABC và
a) A'B' lớn hơn cạnh AB là 10,8 cm
b) A'B' bé hơn cạnh AB là 5,4 cm
cho tam giác ABC = tam giác A'B'C'. Biết góc BC = 10cm; góc AB : góc AC = 4 : 3 và góc AB + góc AC = 14cm. Tính các cạnh của tam giác A'B'C'
Cho tam giác ABC đồng dạng VỚI tam giác A'B'C' AB = 3 cm BC = 5 cm CA = 7 cm tam giác A'B'C' có cạnh nhỏ nhất bằng 4,5 cm Tính các cạnh của của tam giác A'B'C'
ΔABC đồng dạng với ΔA'B'C'
=>\(\dfrac{A'B'}{AB}=\dfrac{A'C'}{AC}=\dfrac{B'C'}{BC}\)
=>\(\dfrac{A'B'}{3}=\dfrac{A'C'}{7}=\dfrac{B'C'}{5}\)
=>A'B'=4,5cm
=>\(\dfrac{A'C'}{7}=\dfrac{B'C'}{5}=\dfrac{3}{2}\)
=>A'C'=10,5cm; B'C'=7,5cm
Đúng 0
Bình luận (0)
Cho tam giác ABC đồng dạng với tam giác A'B'C'. Cho biết AB = 6cm, BC = 10cm, AC = 14cm và chu vi tam giác A'B'C' bằng 45cm. Hãy tính độ dài các cạnh của tam giác A'B'C'
Ta có:
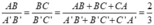
Từ đó tính được A'B' = 9cm, B'C' = 15cm, A'C' = 21cm
Đúng 0
Bình luận (0)
Cho tam giác ABC, có AB=3 cm, BC=5 cm, AC=4 cm.Qua A vẽ a//BC, qua B vẽ b//AC, qua C vẽ c//AB. Gọi A'B'C' theo thứ tự là giao điểm của các đường thẳng b và c, a và c, a và b. Tính độ dài các cạnh của tam giác A'B'C'
1) Cho tam giác abc vuông tại a và tam giác a'b'c' vuông tại A' có BC = 10 cm,AC = 8 cm,B'C'= 5cm,A'C' = 4cm.
a) Tính AB,A'B'.
b) cm: tam giác ABC đồng dạng tam giác A'B'C' (Chi tiết + chính xác)
Cho tam giac ABC và tam giác A'B'C'. M là trung điểm của BC. M' là trung điểm của B'C'. Biết AB=A'B';AC=A'C'; AM=A'M'.CM tam giác ABC=tam giác A'B'C'
Cho tam giác ABC đồng dạng với tam giác A'B'C' AB = 16,2 cm BC = 24,3 cm CA= 32,7 cm Tính các cạnh còn lại của tam giác A'B'C' biết A'B'- AB = 10,8
ΔABC đồng dạng với ΔA'B'C'
=>\(\dfrac{A'B'}{AB}=\dfrac{B'C'}{BC}=\dfrac{A'C'}{AC}\)
A'B'=10,8+16,2=27(cm)
=>\(\dfrac{B'C'}{24.3}=\dfrac{A'C'}{32.7}=\dfrac{16.2}{27}=\dfrac{3}{5}\)
=>B'C'=14,58cm; A'C'=19,62(cm)
Đúng 0
Bình luận (0)




















