Gọi f là hàm số xác định trên tập các số nguyên và thoả mãn các điều kiện:
1)f(x)=0
2)f(1)=3
3)f(x).f(y)=f(x+y)+f(x-y)\(\forall x,y\in Z\)
Tính f(7)
Những câu hỏi liên quan
Gọi f là hàm số xác định trên tập các số nguyên và thoả mãn các điều kiện:
1)f(x)=0
2)f(1)=3
3)f(x).f(y)=f(x+y)+f(x-y) \(\forall\)\(x,y\in Z\)
Gọi f là một hàm xác định trên tập hợp các số nguyên và thỏa mãn ba điều kiện sau
f(0) # 0;
f(1)=3;
f(x)f(y)=f(x+y)+f(x-y)
Tính giá trị của f(7).
theo đề ra ta có f(1)f(0)=f(1+0)+f(1-0) \(\Rightarrow\)3f(0)=3+3\(\Rightarrow\)f(0)=2
f(2)f(0)=f(2+0)+f(2-0) \(\Rightarrow\)2f(2)=2+2\(\Rightarrow\)f(2)=2
f(2)f(1)=f(2+1)+f(2-1) \(\Rightarrow\)2.3=f(3)+3\(\Rightarrow\)f(3)=3
f(3)f(2)=f(3+2)+f(3-2) \(\Rightarrow\)2.3=f(5)+3\(\Rightarrow\)f(5)=3
f(5)f(2)=f(5+2)+f(5-2) \(\Rightarrow\)2.3=f(7)+3\(\Rightarrow\)f(7)=3
Đúng 0
Bình luận (0)
Gọi f là một hàm xác định trên tập hợp các số nguyên và thỏa mãn ba điều kiện sau
f(0) # 0;
f(1)=3;
f(x)f(y)=f(x+y)+f(x-y)
Tính giá trị của f(7)
Ai nhanh đầy đủ mik ti ck nhé
Xác định một hàm số y f(x) thoả mãn đồng thời các điều kiện sauf(x) xác định trên R {1}
lim
x
→
1
f
(
x
)
+
∞
;
lim
x
→
+
∞
f...
Đọc tiếp
Xác định một hàm số y = f(x) thoả mãn đồng thời các điều kiện sau
f(x) xác định trên R\ {1}
lim x → 1 f ( x ) = + ∞ ; lim x → + ∞ f ( x ) = 2 ; lim x → - ∞ f ( x ) = 2
Chẳng hạn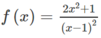 
.
Dễ dàng kiểm tra được rằng f(x) thoả mãn các điều kiện đã nêu
Đúng 0
Bình luận (0)
Xác định một hàm số y = f(x) thoả mãn đồng thời các điều kiện sau
f(x) xác định trên R
y = f(x) liên tục trên (−∞;0) và trên [0;+∞) nhưng gián đoạn tại x = 0
Gọi f là hàm số xác định trên tập các số nguyên và thoả mãn các điều kiện:
1)f(x)=0
2)f(1)=3
3)f(x).f(y)=f(x+y)+f(x-y) \(\forall\)\(x,y\in Z\)
4 tháng 3 2023 lúc 18:13
1. Chứng minh rằng mọi hàm \(f:ℝ\rightarrowℝ\) thỏa mãn \(f\left(xy+x+y\right)=f\left(xy\right)+f\left(x\right)+f\left(y\right),\forall x,y\inℝ\)
2. Xác định tất cả các hàm số \(f\) liên tục trên \(ℝ\) thỏa mãn điều kiện \(f\left(2x-y\right)=2f\left(x\right)-f\left(y\right),\forall x,y\inℝ\)
Cho hàm số yfleft(xright) liên tục trên tập xác định R, và thỏa mãn điều kiện phương trình fleft(xright)0 có 3 nghiệm x-3 ; x0 ; x2. Xét hàm số ygleft(xright)fleft(x^2+4x-mright), tính tổng các giá trị nguyên của tham số min[-10;10] để phương trình gleft(xright)0 có đúng 5 nghiệm phân biệt .A. -6 B. 42 C. 50 D. 6P/s: Kì thi cuối học kỳ 2 lớp 11 trường THPT Phan Huy Chú , thành phố Hà NộiEm xin nhờ sự...
Đọc tiếp
Cho hàm số \(y=f\left(x\right)\) liên tục trên tập xác định R, và thỏa mãn điều kiện phương trình \(f'\left(x\right)=0\) có 3 nghiệm \(x=-3\) ; \(x=0\) ; \(x=2\). Xét hàm số \(y=g\left(x\right)=f\left(x^2+4x-m\right)\), tính tổng các giá trị nguyên của tham số \(m\in[-10;10]\) để phương trình \(g'\left(x\right)=0\) có đúng 5 nghiệm phân biệt .
A. -6 B. 42 C. 50 D. 6
P/s: Kì thi cuối học kỳ 2 lớp 11 trường THPT Phan Huy Chú , thành phố Hà Nội
Em xin nhờ sự giúp đỡ của quý thầy cô giáo và các bạn yêu toán, em cám ơn nhiều ạ!
Cho hàm số y=f(x) xác định và liên tục trên R thõa mãn các điều kiện sau:
\(\hept{\begin{cases}f\left(x\right)>0,\forall x\in R\\f'\left(x\right)=-e^xf^2\left(x\right),\forall x\in R\\f\left(o\right)=\frac{1}{2}\end{cases}}\)
Hãy tính \(f\left(ln2\right)\).