tìm GTLN của A=x - x2
Những câu hỏi liên quan
Cho phân thức A = x2+x+1/x2+2x+1 tìm GTLN
B = x2+x+1/x2+1 tìm GTLN và GTNN
tìm GTNN hoặc GTLN của A = 3x2+2x-3
B = (x2+x+20): x2 +x +5
A=3(x^2+2/3x-1)
=3(x^2+2*x*1/3+1/9-10/9)
=3(x+1/3)^2-10/3>=-10/3
Dấu = xảy ra khi x=-1/3
\(B=1+\dfrac{15}{x^2+x+5}=1+\dfrac{15}{\left(x+\dfrac{1}{2}\right)^2+\dfrac{19}{4}}< =1+15:\dfrac{19}{4}=1+\dfrac{60}{19}=\dfrac{79}{19}\)
Dấu = xảy ra khi x=-1/2
Đúng 2
Bình luận (1)
1. Cho x,y thỏa mãn: x2 + 5y2 - 4xy + 2y = 3. Tìm x,y sao cho x đạt GTLN
2. Cho x,y thỏa mãn: 3x2 + y2 + 2xy + 4 = 7x + 3y
a) Tìm GTNN, GTLN của biểu thức P = x + y
b) Tìm GTNN, GTLN của x
3. Cho x,y thỏa mãn: x2 + 2y2 + 2xy + 7x + 7y + 10 = 0. Tìm GTLN, GTNN của S = x + y
Tìm GTNN, GTLN của biểu thức: A = (x2 + x +1)/(x2 - x +1)
3A=3(x^2-x+1)/(x^2+x+1)
3A-1=(3x^2-3x+3)/(x^2+x+1)-1
3A-1=(3x^2-3x+3-x^2-x-1)/(x^2+x+1)
3A-1=(2x^2-4x+2)/(x^2+x+1)
3A-1=2(x-1)^2/(x^2+x+1)>=0
=>3A>=1
A>=1/3
=>GTNN của A là 1/3 khi x-1=0 hay x=1
A-3=(x^2-x+1)/(x^2+x+1)-3
A-3=(x^2-x+1-3x^2-3x-3)/(x^2+x+1)
A-3=(-2x^2-4x-2)/(x^2+x+1)
A-3=-2(x+1)^2/(x^2+x+1)<=0
=>A<=3
=>GTLN của A=3 khi x=-1
Đúng 0
Bình luận (0)
A=(-x2+x-11)/(x2-2*x+1)
tìm gtln,gtnn của biểu thức giúp e với ạ
. Tìm GTLN, GTNN của biểu thức:1) Tìm GTNN của biểu thức: a) A x2 - 7x +11.b) D x - 2 + x - 3 .c) C 3 - 4x .x2 +1d) B -5 .x2 - 4x + 7e) x2 - x +1 .M + x +1x2f) P x 1 x 2 x 3 x 6 .2) Tìm GTLN của biểu thức 2x 2 + 4x + 9 b)A x 2 + 2x + 4 . a)B −5 x 2+ 22 x − 25 2x 2 + 4x + 9 x 2+ 4 x + 4b)A x 2 + 2x + 4 . c) C (x2 - 3x +1)(21+ 3x - x2 ) .d) D 6x - 8 .x2 +1
Đọc tiếp
. Tìm GTLN, GTNN của biểu thức:
1) Tìm GTNN của biểu thức:
a) A = x2 - 7x +11. | b) D = x - 2 + x - 3 . |
c) C = 3 - 4x . x2 +1 | d) B = -5 . x2 - 4x + 7 |
e) x2 - x +1 . M = + x +1 x2 | f) P x 1 x 2 x 3 x 6 . |
2) Tìm GTLN của biểu thức
|
| 2x 2 + 4x + 9 |
|
b) | A = x 2 + 2x + 4 . | ||
|
| ||||||||||||||||||||
c) C = (x2 - 3x +1)(21+ 3x - x2 ) . | d) D = 6x - 8 . x2 +1 | ||||||||||||||||||||
1:
a: =x^2-7x+49/4-5/4
=(x-7/2)^2-5/4>=-5/4
Dấu = xảy ra khi x=7/2
b: =x^2+x+1/4-13/4
=(x+1/2)^2-13/4>=-13/4
Dấu = xảy ra khi x=-1/2
e: =x^2-x+1/4+3/4=(x-1/2)^2+3/4>=3/4
Dấu = xảy ra khi x=1/2
f: x^2-4x+7
=x^2-4x+4+3
=(x-2)^2+3>=3
Dấu = xảy ra khi x=2
2:
a: A=2x^2+4x+9
=2x^2+4x+2+7
=2(x^2+2x+1)+7
=2(x+1)^2+7>=7
Dấu = xảy ra khi x=-1
b: x^2+2x+4
=x^2+2x+1+3
=(x+1)^2+3>=3
Dấu = xảy ra khi x=-1
Đúng 0
Bình luận (0)
Tìm GTNN hoặc GTLN của các biểu thức sau:
a) A = x2 + 3x + 4
b) B = 2x2 - x + 1
c) C = 5x - x2 + 4
d) D = x2 + 5y2 - 2xy + 4y + 3
a: Ta có: \(A=x^2+3x+4\)
\(=x^2+2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{7}{4}\)
\(=\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{3}{2}\)
Đúng 0
Bình luận (0)
Bài 6: a)Tìm GTLN, GTNN của biểu thức sau:a. x2 – 6x +11 b. –x2 + 6x – 11 c) Chứng minh rằng: x2 + 2x + 2 0 với x Z
Đọc tiếp
Bài 6: a)Tìm GTLN, GTNN của biểu thức sau:
a. x2 – 6x +11 b. –x2 + 6x – 11
c) Chứng minh rằng: x2 + 2x + 2 > 0 với x 
c: \(=\left(x+1\right)^2+1>0\forall x\)
Đúng 0
Bình luận (0)
Trả lời:
a, \(x^2-6x+11=x^2-6x+9+2=\left(x-3\right)^2+2\ge2\forall x\)
Dấu "=" xảy ra khi x - 3 = 0 <=> x = 3
Vậy GTNN của biểu thức bằng 2 khi x = 3
b, \(-x^2+6x-11=-\left(x^2-6x+11\right)=-\left(x^2-6x+9+2\right)=-\left[\left(x-3\right)^2+2\right]\)
\(=-\left(x-3\right)^2-2\le-2\forall x\)
Dấu "=" xảy ra khi x - 3 = 0 <=> x = 3
Vậy GTLN của biểu thức bằng - 2 khi x = 3
c, \(x^2+2x+2=x^2+2x+1+1=\left(x+1\right)^2+1\ge1>0\forall x\inℤ\) (đpcm)
Dấu "=" xảy ra khi x + 1 = 0 <=> x = - 1
Tìm GTLN của BT
-x2+2xy-4y2+2x+10y-8
-x2-y2+xy+x+y
Tìm GTLN của hàm số y = x - x 2 + 1 ?
A. 0
B. 1
C. Không tồn tại
D. Không có đáp án
Tập xác định R.
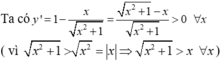
Ta có bảng biến thiên:
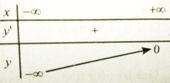
Hàm số không có GTLN trên R . Chọn đáp án C.
Đúng 0
Bình luận (0)