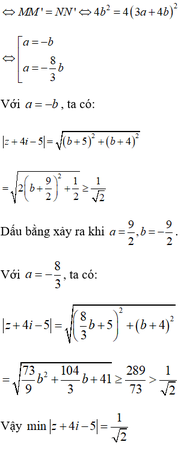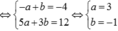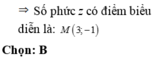Tìm số điểm biểu diễn của số phức z sao cho \(z^4\) - 1 = 0

Những câu hỏi liên quan
Cho M(1; 2) là điểm biểu diễn số phức z. Tìm tọa độ của điểm N biểu diễn số phức w = z + 2 z ¯
A. N (3; -2)
B. N (2; -3)
C. N (2; 1)
D. N (2; 3)
Cho số phức z và số phức liên hợp của nó
z
¯
có điểm biểu diễn là M, M’. Số phức z(4+3i) và số phức liên hợp của nó có điểm biểu diễn lần lượt là N, N’. Biết rằng 4 điểm M, N, M’, N’ tạo thành hình chữ nhật. Tìm giá trị nhỏ nhất của biểu thức |z + 4i -5|
A
.
1
2
B
.
2
5...
Đọc tiếp
Cho số phức z và số phức liên hợp của nó z ¯ có điểm biểu diễn là M, M’. Số phức z(4+3i) và số phức liên hợp của nó có điểm biểu diễn lần lượt là N, N’. Biết rằng 4 điểm M, N, M’, N’ tạo thành hình chữ nhật. Tìm giá trị nhỏ nhất của biểu thức |z + 4i -5|
A . 1 2
B . 2 5
C . 5 34
D . 4 13
Đáp án A
Giả sử ![]()
Ta có M(a;b) và M'(a;-b)
Khi đó ![]()
Suy ra ![]() và
và ![]()
Do 4 điểm M, N, M’, N’ tạo thành hình thang cân nhận Ox làm trục đối xứng nên 4 điểm đó lập thành hình chữ nhật
![]()

Với a = -b, ta có
![]()
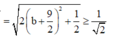
Dấu bằng xảy ra khi 
Với  ta có
ta có 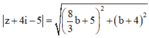
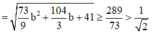
Vậy 
Đúng 0
Bình luận (0)
Cho số phức z và số phức liên hợp của nó
z
có điểm biểu diễn là M, M’. Số phức
z
.
(
4
+
3
i
)
và số phức liên hợp của nó có điểm biểu diễn lần lượt là N, N’. Biết rằng 4 điểm M, N, M’, N’ tạo thành hình chữ nhật. Tìm giá trị nhỏ nhất của biểu thức
|
z
+
4
i
-
5
|
. A.
1
2...
Đọc tiếp
Cho số phức z và số phức liên hợp của nó z có điểm biểu diễn là M, M’. Số phức z . ( 4 + 3 i ) và số phức liên hợp của nó có điểm biểu diễn lần lượt là N, N’. Biết rằng 4 điểm M, N, M’, N’ tạo thành hình chữ nhật. Tìm giá trị nhỏ nhất của biểu thức | z + 4 i - 5 | .
A. 1 2
B. 2 5
C. 5 34
D. 4 13
Cho M(1;2) là điểm biểu diễn số phức z. Tìm tọa độ của điểm N biểu diễn số phức w = z + 2 z ¯ .
A. N = (3;-2)
B. N = (2;-3)
C. N = (2;1)
D. N = (2;3)
Cho số phức z thỏa mãn:
z
(
1
+
2
i
)
-
z
¯
(
2
-
3
i
)
-
4
+
12
i
. Tìm tọa độ điểm M biểu diễn số phức z.
Đọc tiếp
Cho số phức z thỏa mãn: z ( 1 + 2 i ) - z ¯ ( 2 - 3 i ) = - 4 + 12 i . Tìm tọa độ điểm M biểu diễn số phức z.
![]()
![]()
![]()
![]()
Cho số phức z thỏa (2i-1)z4-3i.Tìm điểm M là điểm biểu diễn của số phức
z
-
A. M(2 ;1) B. M(2 ;-1) C. M(-2;1) D. M(-2;-1)
Đọc tiếp
Cho số phức z thỏa (2i-1)z=4-3i.Tìm điểm M là điểm biểu diễn của số phức z -
A. M(2 ;1)
B. M(2 ;-1)
C. M(-2;1)
D. M(-2;-1)
Gọi M,N lần lượt là các điểm biểu diễn của số phức z= 1 i, z'= 2 3i. Tìm số phức w có điểm biểu diễn là Q sao cho vector MN 3 vector MQ =vector 0A. w=-1/3iB. w= 4/3 5/3iC. w= -2/3-1/3iD. w=2/3 1/3i
\(M\left(1;1\right)\) ; \(N\left(2;3\right)\)
Gọi \(w=x+yi\Rightarrow Q\left(x;y\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{MN}=\left(1;2\right)\\\overrightarrow{MQ}=\left(x-1;y-1\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MN}+3\overrightarrow{MQ}=\left(3x-2;3y-1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\) \(\Rightarrow w=\dfrac{2}{3}+\dfrac{1}{3}i\)
Đúng 0
Bình luận (0)
Biết tập hợp điểm M biểu diễn số phức z là đường thẳng (d): 3x + 2y – 5 = 0. Tìm số phức z sao cho phần thực và phần ảo bằng nhau
A. z = 5 + 5i
B. z = 5 – 5i
C. z = -5 + 5i
D. z = 1 + i
Trong mặt phẳng phức Oxy, các số phức z thỏa
z
+
2
i
-
1
z
+
i
. Tìm số phức z được biểu diễn bởi điểm M sao cho MA ngắn nhất với A(1;3)
Đọc tiếp
Trong mặt phẳng phức Oxy, các số phức z thỏa z + 2 i - 1 = z + i . Tìm số phức z được biểu diễn bởi điểm M sao cho MA ngắn nhất với A(1;3)
![]()
![]()
![]()
![]()