Số nào trong ba số \(-1;2;3\) nghiệm đúng mỗi phương trình sau :
\(\left|x\right|=x\left(1\right)\) \(x^2+5x+6=0\left(2\right)\) \(\dfrac{6}{1-x}=x+4\left(3\right)\)
Những câu hỏi liên quan
3.010.800: số ba trong mỗi số thuộc hàng nào? lớp nào?
342.601: số ba trong mỗi số thuộc hàng nào? lớp nào?
630.002: số ba trong mỗi số thuộc hàng nào? lớp nào?
2.489.073: số ba trong mỗi số thuộc hàng nào? lớp nào?
3.010.800 có số 3 thuộc hàng triệu. Lớp triệu.
342.601 có số 3 thuộc hàng trăm nghìn. Lớp nghìn.
630.002 có số 3 thuộc hàng chục nghìn. Lớp nghìn.
2.489.073 có số 3 thuộc hàng đơn vị. Lớp đơn vị
Đúng 0
Bình luận (0)
3.010.800 số 3 trong số thuộc hàng triệu.
342.601 số 3 trong số thuộc hàng trăm nghìn.
630.002 số 3 trong số thuộc hàng chục nghìn.
2.489.073 số 3 trong số thuộc hàng đơn vị.
Đúng 0
Bình luận (0)
1)Trong 3 số tự nhiên liên tiếp có 1 số là 19.Hỏi ba số tự nhiên đó là ba số nào?
Trong 3 số tự nhiên liên tiếp có 1 số là 19\(\Rightarrow\)số 19 là số đầu, số giữa hoặc số cuối
- 19 là số đầu\(\Rightarrow\)ba số tự nhiên đó là 19,20,21
- 19 là số giữa\(\Rightarrow\)ba số tự nhiên đó là: 18,19,20
- 19 là số cuối\(\Rightarrow\)ba số tự nhiên đó là; 17,18,19
Vậy là có ba trường hợp
Hk tốt
Đúng 0
Bình luận (0)
Cho ba số nguyên a, b, c và biết:
\(a > 2;b < - 7; - 1 < c < 1\).
Hỏi trong các số nói trên, số nào là số nguyên dương, số nào là số nguyên âm và số nào bằng 0?
\(a > 2\), mà \(2 > 0\) nên \(a >0\). Vậy \(a > 0\) và là số nguyên dương.
\(b < - 7\), mà \(-7 < 0\) nên \(b<0\). Vậy \(b < 0\) và là số nguyên âm.
\( - 1 < c < 1\) nên số c là số nằm giữa hai số -1 và 1. Mà chỉ có số 0 là số nguyên nằm giữa 2 số này nên c phải là số 0.
Đúng 0
Bình luận (0)
trong ba số x,y,z số nào là số 0 khi x,y,z là ba số gồm 1 số dương ,1 số âm và 1 số 0.
|x|=y.(y+z)
x=0 khi y và z là hai số đối nhau
y không thể là số 0
z=0 khi giá trị tuyệt đối của x =y2
Đúng 0
Bình luận (0)
x = 0 khi y và z là 2 số đối nhau
y không thể là số 0
z = 0 khi giá trị tuyệt đối của x = y2
Đúng 0
Bình luận (0)
Trong ba số nguyên có hai số nguyên âm và 1 số nguyên dương hỏi ba số đó là loại số nào biết a*b=c ngũ 2010
Minh nghĩ ra ba phân số có tổng bằng 1, một trong ba phân số đó là 1/6. Em hãy co biết hai phân số còn lại có thể là những phân số nào ?
Tổng của 2 phân số còn lại là: 1 - 1/6 = 5/6
Mà: 5/6 = 1/6 + 2/3 = 1/3 + 1/2
=> hai phân số còn lại có thể là: 1/6 và 2/3 ; 1/3 và 1/2
Đúng 1
Bình luận (0)
Số nào trong ba số -1, 2 và -3 nghiệm đúng mỗi phương trình sau?
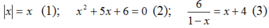
+ Xét phương trình |x| = x
Tại x = -1: VT = |x| = |-1| = 1; VP = x = -1
⇒ 1 ≠ -1 nên -1 không phải nghiệm của phương trình |x| = x.
Tại x = 2: VT = |x| = |2| = 2; VP = x = 2
⇒ VT = VP = 2 nên 2 là nghiệm của phương trình |x| = x.
Tại x = -3: VT = |x| = |-3| = 3; VP = x = -3
⇒ 3 ≠ -3 nên -3 không phải nghiệm của phương trình |x| = x.
Vậy chỉ có 2 là nghiệm đúng của phương trình |x| = x.
+ Xét phương trình x2 + 5x + 6 = 0.
Tại x = -1 có: VT = x2 + 5x + 6 = (-1)2 + 5.(-1) + 6 = 2 ≠ 0
⇒ -1 không phải nghiệm của phương trình x2 + 5x + 6 = 0.
Tại x = 2 có: VT = x2 + 5x + 6 = 22 + 5.2 + 6 = 20 ≠ 0
⇒ 2 không phải nghiệm của phương trình x2 + 5x + 6 = 0.
Tại x = -3 có: VT = x2 + 5x + 6 = (-3)2 + 5.(-3) + 6 = 0
⇒ -3 là nghiệm đúng của phương trình x2 + 5x + 6 = 0.
+ Xét phương trình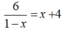 
Tại x = -1 có: VT =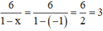 
, VP = x + 4 = (-1) + 4 = 3
⇒ VT = VP = 3 nên x = -1 là nghiệm đúng của phương trình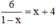 
Tại x = 2 có: VT =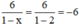 
; VP = x + 4 = 2 + 4 = 6
⇒ -6 ≠ 6 nên x = 2 không phải nghiệm của phương trình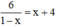 
Tại x = -3 có VT =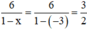 
; VP = x + 4 = -3 + 4 = 1.
⇒ 
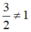nên x = -3 không phải nghiệm của phương trình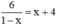 
Đúng 0
Bình luận (0)
trong ba số a,b,c có 1 số dương , 1 số bằng 0 , một số âm. Hỏi ba số đó là loại số nào nếu biết rằng :\(|a|=b^2\cdot \left(b-c\right)\)
Cho tập hợp A
1
;
2
;
3
;
.
.
.
.
.
;
10
. Chọn ngẫu nhiên ba số từ A. Tìm xác suất để trong ba số chọn ra không có hai số nào là hai số nguyên liên tiếp
Đọc tiếp
Cho tập hợp A = 1 ; 2 ; 3 ; . . . . . ; 10 . Chọn ngẫu nhiên ba số từ A. Tìm xác suất để trong ba số chọn ra không có hai số nào là hai số nguyên liên tiếp
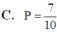
Đáp án D
Chon 3 số bất kì có C 10 3 = 120 cách
TH1: 3 số chọn ra là 3 số tự nhiên liên tiếp có 8 cách
TH2: 3 số chọn ra là 2 số tự nhiên liên tiếp
+) 3 số chọn ra có cặp (1;2) hoặc (9;10) có 2.7 = 14 cách
+) 3 số chọn ra có cặp ( 2 ; 3 ) ; ( 3 ; 4 ) ; . . . . ( 8 ; 9 ) có 6.6 = 36 cách
Vậy xác suất cần tìm là
Đúng 0
Bình luận (0)
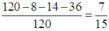
Trong ba số nguyên a , b , c có hai số nguyên âm và một số nguyên dương . Hỏi ba số đó là loại số nào biết rằng \(\frac{ab}{c^{2016}}\) =1.