Lập phương trình mặt phẳng (P) đi qua 3 điểm \(A\left(-1;-3;2\right);B\left(-2;1;1\right);C\left(0;1;-1\right)\) ?

Những câu hỏi liên quan
Cho A(1,2,-3), B(3,0,1) , denta :left{{}begin{matrix}x-1+2ty2-tztend{matrix}right.(P): x+y+z-30a) Lập phương trình mặt phẳng (Q) đi qua điểm A và chứa đường thẳng dentab) Lập phương trình mặt phẳng (Q) đi qua điểm A và song song với đường thẳng denta và vuông góc với mặt phẳng (P)c) Lập phương trình đường thẳng d nằm trên mặt phẳng (P) cắt và vuông góc với dentad) Lập phương trình đường thẳng d đi qua điểm A cắt denta tại M, cắt mặt phẳng (P) tại N sao cho M là trung điểm AN
Đọc tiếp
Cho A(1,2,-3), B(3,0,1) , denta :\(\left\{{}\begin{matrix}x=-1+2t\\y=2-t\\z=t\end{matrix}\right.\)
(P): x+y+z-3=0
a) Lập phương trình mặt phẳng (Q) đi qua điểm A và chứa đường thẳng denta
b) Lập phương trình mặt phẳng (Q) đi qua điểm A và song song với đường thẳng denta và vuông góc với mặt phẳng (P)
c) Lập phương trình đường thẳng d nằm trên mặt phẳng (P) cắt và vuông góc với denta
d) Lập phương trình đường thẳng d đi qua điểm A cắt denta tại M, cắt mặt phẳng (P) tại N sao cho M là trung điểm AN
a.
Chọn \(C\left(1;1;1\right)\) là 1 điểm thuộc denta
\(\Rightarrow\overrightarrow{AC}=\left(0;-1;4\right)\)
Đường thẳng denta có \(\overrightarrow{u_{\Delta}}=\left(2;-1;1\right)\) là 1 vtcp
\(\Rightarrow\left[\overrightarrow{AC};\overrightarrow{u_{\Delta}}\right]=\left(3;8;2\right)\)
\(\Rightarrow\left(Q\right)\) nhận \(\left(3;8;2\right)\) là 1 vtpt
Phương trình (Q):
\(3\left(x-1\right)+8\left(y-2\right)+2\left(y+3\right)=0\)
b.
Mặt phẳng (P) nhận \(\overrightarrow{n_{\left(P\right)}}=\left(1;1;1\right)\) là 1 vtpt
Ta có: \(\left[\overrightarrow{u_{\Delta}};\overrightarrow{n_{\left(P\right)}}\right]=\left(-2;-1;3\right)\)
Mặt phẳng (Q) nhận (2;1;-3) là 1 vtpt
Phương trình (Q):
\(2\left(x-1\right)+1\left(y-2\right)-3\left(z+3\right)=0\)
Đúng 2
Bình luận (0)
c.
Gọi M là giao điểm denta và (P) thì tọa độ M thỏa:
\(-1+2t+2-t+t-3=0\Rightarrow t=1\)
\(\Rightarrow M\left(1;1;1\right)\)
\(\left[\overrightarrow{n_{\left(P\right)}};\overrightarrow{u_{\Delta}}\right]=\left(2;1;-3\right)\)
Đường thẳng d nhận (2;1;-3) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=1+2t\\y=1+t\\z=1-3t\end{matrix}\right.\)
d.
Do M thuộc denta nên tọa độ có dạng: \(M\left(-1+2t;2-t;t\right)\)
M là trung điểm AN \(\Rightarrow N\left(-3+4t;2-2t;2t+3\right)\)
N thuộc (P) nên: \(-3+4t+2-2t+2t+3-3=0\Rightarrow t=\dfrac{1}{4}\)
\(\Rightarrow\overrightarrow{MN}=\left(-2+2t;-t;t+3\right)=\left(-\dfrac{3}{2};-\dfrac{1}{4};\dfrac{13}{4}\right)=-\dfrac{1}{4}\left(6;1;13\right)\)
Phương trình d: \(\left\{{}\begin{matrix}x=1+6t\\y=2+t\\z=-3+13t\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Trong không gian Oxyz
a) Lập phương trình của các mặt phẳng tọa độ \(\left(Oxy\right),\left(Oyz\right),\left(Oxz\right)\) ?
b) Lập phương trình của các mặt phẳng đi qua điểm \(M\left(2;6;-3\right)\) và lần lượt song song với các mặt phẳng tọa độ ?
Giải:
a) Mặt phẳng (Oxy) qua điểm O(0 ; 0 ; 0) và có vectơ pháp tuyến (0 ; 0 ; 1) và là vectơ chỉ phương của trục Oz. Phương trình mặt phẳng (Oxy) có dạng:
0.(x - 0) +0.(y - 0) +1.(z - 0) = 0 hay z = 0.
Tương tự phương trình mặt phẳng (Oyz) là : x = 0 và phương trình mặt phẳng (Ozx) là: y = 0.
b) Mặt phẳng (P) qua điểm M(2; 6; -3) song song với mặt phẳng Oxy nhận (0 ; 0 ; 1) làm vectơ pháp tuyến. Phương trình mặt phẳng (P) có dạng: z +3 = 0.
Tương tự mặt phẳng (Q) qua M và song song với mặt phẳng Oyz có phương trình x - 2 = 0.
Mặt phẳng qua M song song với mặt phẳng Oxz có phương trình y - 6 = 0.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2 ;-1 ;3) và song song với mặt phẳng (Q): A. B. x - 2y + 3z - 15 0 C. 3x - 6y + 2z - 18 0 D. 3x - 6y + 2z + 18 0
Đọc tiếp
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2 ;-1 ;3) và song song với mặt phẳng (Q): 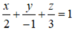
A. ![]()
B. x - 2y + 3z - 15 = 0
C. 3x - 6y + 2z - 18 = 0
D. 3x - 6y + 2z + 18 = 0
Đáp án C
Phương trình mặt phẳng (Q) viết lại dưới dạng: 3x - 6y + 2z - 6 = 0
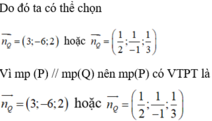
Suy ra đáp án B sai. Trong ba đáp án còn lại chỉ có mặt phẳng ở đáp án C đi qua điểm A.
Đúng 0
Bình luận (0)
Lập phương trình mặt phẳng (P) đi qua điểm M(1; -3; 2) và song song với mặt phẳng (Q): x – z = 0.
Chọn n P → = n Q → = (1; 0; −1)
Phương trình của (P) là: (x – 1) – (z – 2) = 0 hay x – z + 1 = 0.
Đúng 0
Bình luận (0)
Lập phương trình mặt phẳng (P) đi qua ba điểm A(-1; -3; 2), B(-2; 1; 1) và C(0; 1; -1).
Ta có: AB → (−1; 4; −1); AC → (1; 4; −3)
⇒ AB → ∧ AC →
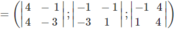
= (−8; −4; −8)
Suy ra có thể chọn n P → = (2; 1; 2)
Phương trình của (P) là: 2x + (y – 1) + 2(z + 1) = 0 hay 2x + y + 2z + 1 = 0.
Đúng 0
Bình luận (0)
Lập phương trình mặt phẳng ( α ) đi qua hai điểm A(0; 1; 0) , B(2; 3; 1) và vuông góc với mặt phẳng ( β ): x + 2y – z = 0 .
Mặt phẳng ( α ) đi qua hai điểm A, B và vuông góc với mặt phẳng ( β ): x + 2y – z = 0.
Vậy hai vecto có giá song song hoặc nằm trên ( α ) là AB → = (2; 2; 1) và n β → = (1; 2; −1).
Suy ra ( α ) có vecto pháp tuyến là: n α → = (−4; 3; 2)
Vậy phương trình của ( α ) là: -4x + 3(y – 1) + 2z = 0 hay 4x – 3y – 2z + 3 = 0
Đúng 0
Bình luận (0)
Lập phương trình mặt phẳng (P) đi qua điểm \(M\left(1;-3;2\right)\) và song song với mặt phẳng \(\left(Q\right):x-z=0\) ?
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua ba điểm A(1;0;1), B(0;-1;-3), C(2;1;3)
A. x - y - 1 = 0
B. x - y + 1 = 0
C. x + z - 2 = 0
D. x + y - 1 = 0
Đáp án A
Từ giả thiết ta suy ra:
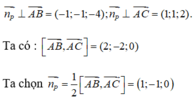
Từ đó suy ra phương trình của mặt phẳng (P) là: 1(x - 1) - 1(y - 0) = 0 ⇔ x - y - 1 = 0
Đúng 0
Bình luận (0)
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua ba điểm A(1 ;0 ;1), B(0 ;-1 ;-3), C(3 ;2 ;5).
A. x - y - 1 = 0
B. x - y + 1 = 0
C. x + z - 2 = 0
D. x + y - 1 = 0
Đáp án A
Từ giả thiết ta suy ra
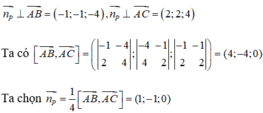
Mặt khác (P) đi qua điểm A(1 ;0 ;1) nên ta có phương trình của mặt phẳng (P) là : 1(x - 1) - 1(y - 0) = 0 <=> x - y - 1 = 0.
Vậy đáp án đúng là A.
Đúng 0
Bình luận (0)









