Đáp án A
Từ giả thiết ta suy ra:
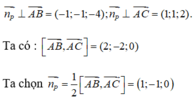
Từ đó suy ra phương trình của mặt phẳng (P) là: 1(x - 1) - 1(y - 0) = 0 ⇔ x - y - 1 = 0
Đáp án A
Từ giả thiết ta suy ra:
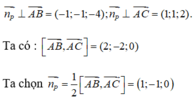
Từ đó suy ra phương trình của mặt phẳng (P) là: 1(x - 1) - 1(y - 0) = 0 ⇔ x - y - 1 = 0
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua hai điểm A(1;0;1), B(2;1;3), đồng thời vuông góc với mặt phẳng (Q): x + y - 3z = 0
A. x - y - 1 = 0
B. x + y - 1 = 0
C. x + z - 1 = 0
D. x + y - 3z + 2 = 0
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm B(2;1;3) đồng thời vuông góc với hai mặt phẳng (Q): x + y - 3z = 0, (R): 2x - y - z = 0
A. 4x + 5y + 3z + 22 = 0
B. 4x - 5y + 3z - 12 = 0
C. 2x + y + 3z - 22 = 0
D. 4x + 5y + 3z - 22 = 0
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2;1;3), vuông góc với mặt phẳng (Q): x + y - 3z = 0 đồng thời (P) song song với trục Oz
A. x + y - 3 = 0
B. x - y - 1 = 0
C. 2x + y + 3z - 1 = 0
D. x - y + 1 = 0
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua ba điểm A(1 ;0 ;1), B(0 ;-1 ;-3), C(3 ;2 ;5).
A. x - y - 1 = 0
B. x - y + 1 = 0
C. x + z - 2 = 0
D. x + y - 1 = 0
Trong không gian Oxyz, lập phương trình của mặt cầu (S) đi qua 3 điểm O, A(2;0;0), B(0;2;0) và tâm thuộc mặt phẳng (P): x + y + z - 3 = 0
A. ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 3
B. ( x + 1 ) 2 + ( y + 1 ) 2 + ( z + 1 ) 2 = 3
C. ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 9
D. ( x + 1 ) 2 + ( y + 1 ) 2 + ( z + 1 ) 2 = 9
Trong không gian với hệ toạ độ Oxyz, cho điểm A(1;-2;3) và hai mặt phẳng (P):x+y+z+1=0, (Q):x-y+z-2=0. Phương trình nào dưới đây là phương trình đường thẳng đi qua A, song song với (P) và (Q)?
A. x = - 1 + t y = 2 z = - 3 - t
B. x = 1 y = - 2 z = 3 - 2 t
C. x = 1 + 2 t y = - 2 z = 3 + 2 t
D. x = 1 + t y = - 2 z = 3 - t
Trong không gian Oxyz, cho hai mặt phẳng (P): x - 2y - z + 3 = 0,
(Q): 2x + y + z - 1 = 0. Mặt phẳng (R) đi qua điểm M(1;1;1) và chứa
giao tuyến của (P) và (Q).
Phương trình của (R): m.(x - 2y - z + 3) + (2x + y + z -1) = 0. Khi đó giá trị của m là
A. 3
B. 1 3
C. -1
D. -3
Trong không gian Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a,b,c khác 0 Biết rằng mặt phẳng (ABC) đi qua điểm M 2 3 ; 4 3 ; 4 3 và tiếp xúc với mặt cầu (S): ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 2 ) 2 = 1 Thể tích khối tứ diện OABC bằng
A. 4
B. 6
C. 9
D. 12
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2 ;1 ;-3), vuông góc với mặt phẳng (Q): x + y - 3z = 0 đồng thời (P) song song với trục Oz.
A. x + y - 3 = 0
B. x - y - 1 = 0
C. 2x + y - 3z - 1 = 0
D. x - y + 1 = 0