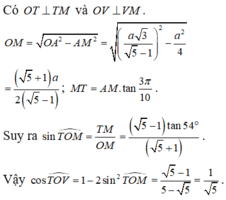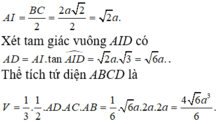Tính sin của góc tạo bởi hai mặt kề (tức là hai mặt có một cạnh chung) của một tứ diện đều ?

Những câu hỏi liên quan
Tính sin của góc tạo bởi hai mặt kề nhau (tức là hai mặt có một cạnh chung) của một tứ diện đều.
Cho tứ diện đều ABCD cạnh bằng a. Gọi M và N theo thứ tự là trung điểm của AB và CD. Khi đó góc giữa hai mặt (CAB) và (DAB) bằng ∠ CMD = 2 ∠ CMN
Ta có: ![]()
Do đó: 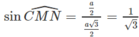
Từ đó suy ra: ![]()
Đúng 0
Bình luận (0)
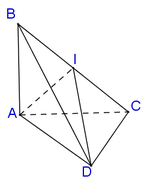
Cho hình tứ diện đều ABCD có cạnh bằng a. Côsin của góc tạo bởi hai mặt có chung một cạnh của tứ diện đều bằng A.
2
3
B.
1
3
C.
2
4
D.
2
8
Đọc tiếp
Cho hình tứ diện đều ABCD có cạnh bằng a. Côsin của góc tạo bởi hai mặt có chung một cạnh của tứ diện đều bằng
A. 2 3
B. 1 3
C. 2 4
D. 2 8
Đáp án B
Gọi O,M lần lượt là trọng tâm tam giác BCD, trung điểm cạnh CD. Khi đó
![]()
Do đó
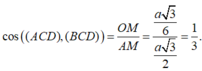
Đúng 0
Bình luận (0)
Cho hình tứ diện đều ABCD có cạnh bằng a. Côsin của góc tạo bởi hai mặt có chung một cạnh của tứ diện đều bằng A.
2
3
B.
1
3
C.
2
4
D.
2
8
Đọc tiếp
Cho hình tứ diện đều ABCD có cạnh bằng a. Côsin của góc tạo bởi hai mặt có chung một cạnh của tứ diện đều bằng
A. 2 3
B. 1 3
C. 2 4
D. 2 8
Cho hình tứ diện đều ABCD có cạnh bằng a. Côsin của góc tạo bởi hai mặt có chung một cạnh của tứ diện đều bằng A.
2
3
B.
1
3
C.
2
4
D.
2
8
Đọc tiếp
Cho hình tứ diện đều ABCD có cạnh bằng a. Côsin của góc tạo bởi hai mặt có chung một cạnh của tứ diện đều bằng
A. 2 3
B. 1 3
C. 2 4
D. 2 8
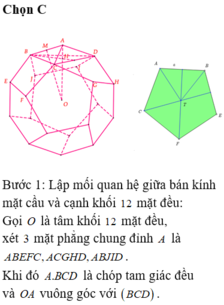
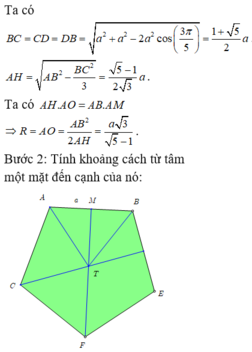
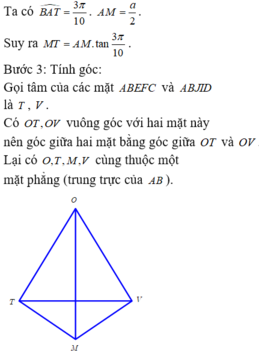
Cho hình thập nhị diện đều (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng có chung một cạnh của thập nhị diện đều bằng A.
5
-
1
2
B.
5
-
1
4
C.
1...
Đọc tiếp
Cho hình thập nhị diện đều (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng có chung một cạnh của thập nhị diện đều bằng
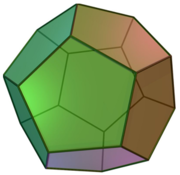
A. 5 - 1 2
B. 5 - 1 4
C. 1 5
D. 1 2
Chứng minh:
a, Diện tích của một tam giác bằng nửa tích của hai cạnh nhân với sin của góc nhọn tạo bởi các đường thẳng chứa hai cạnh ấy
b, Diện tích của tứ giác bất kỳ bằng nửa tích của hai đường chéo nhân với sin của góc nhọn tạo bởi hai đường chéo
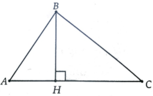
a, Giả sử tam giác ABC có A ^ < 90 0 kẻ đường cáo BH. Ta có BH=AB.sin A ^
=> S ∆ A B C = 1 2 A C . B H = 1 2 A B . A C . sin A
b, Giả sử tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O có
A
O
B
^
=
α
<
90
0
. Kẻ AH
⊥
BD, tại H và CK
⊥
BD tại K
Ta có: AH = OA.sinα
=> S A B D = 1 2 B D . A H = 1 2 B D . O A . sin α
Tương tự: S C B D = 1 2 B D . C K = 1 2 B D . O C . sin α
=> S A B C D = S A B D + S C B D = 1 2 B D . O A . sin α + 1 2 B D . O C . sin α = 1 2 B D . A C . sin α

Đúng 1
Bình luận (0)
chứng minh rằng:
a) diện tích của một tam giác bằng nửa tích của hai cạnh nhân với sin của góc nhọn tạo bởi các đường thẳng chứa 2 cạnh ấy
b) Diện tích của một hình bình hành bằng tích của hai cạnh kề nhân với sin của góc nhọn tạo bởi các đường thẳng chứa 2 cạnh ấy
GIẢI GIÚP MIK VS M.N
A) Vẽ t/g ABC (A là góc nhọn), đường cao BH.
1/2.AB.AC.sinA = 1/2.AB.AC.(BH/AB) = 1/2.BH.AC = S(ABC)
Đúng 1
Bình luận (0)
Chứng minh
Diện tích của một hình bình hành bằng tích của hai cạnh kề nhân với sin của góc nhọn tạo bởi các đường thẳng chứa hai cạnh ấy
Gọi hình bình hành đó là ABCD , từ A kẻ đường cao AH xuống cạnh CD (H thuộc CD)
Ta có : \(AH=AD.sinD\)
\(\Rightarrow S_{ABCD}=CD.AH=CD.AD.sinD\)
Vậy ta có điều phải chứng minh
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có cạnh AB,AC,AD đôi một vuông góc. Biết rằng
A
B
A
C
2
a
và góc tạo bởi hai mặt phẳng (DCB) và (ABC) bằng
60
0
.
Tính thể tích khối tứ diện ABCD. A.
2
6
a
3
3
B....
Đọc tiếp
Cho tứ diện ABCD có cạnh AB,AC,AD đôi một vuông góc. Biết rằng A B = A C = 2 a và góc tạo bởi hai mặt phẳng (DCB) và (ABC) bằng 60 0 . Tính thể tích khối tứ diện ABCD.
A. 2 6 a 3 3
B. 4 6 a 3 3
C. 2 6 a 3
D. 4 6 a 3