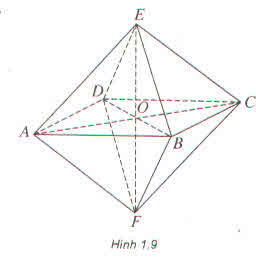
Cho tứ diện đều ABCD cạnh bằng a. Gọi M và N theo thứ tự là trung điểm của AB và CD. Khi đó góc giữa hai mặt (CAB) và (DAB) bằng \(\widehat{CMD}=2\widehat{CMN}\)
Ta có :
\(CM=\dfrac{a\sqrt{3}}{2};CN=\dfrac{a}{2}\)
Do đó :
\(\sin\widehat{CMN}=\dfrac{\dfrac{a}{2}}{\dfrac{a\sqrt{3}}{2}}=\dfrac{1}{\sqrt{3}}\)
Từ đó suy ra :
\(\sin\widehat{CMD}=\dfrac{2\sqrt{2}}{3}\)
Chứng minh rằng tâm của các mặt của các hình tứ diện đều là các đỉnh của một hình tứ diện đều ?
Cho khối bát diện đều ABCDEF (h.1.9). Gọi O là giao điểm của AC, BD, M và N theo thứ tự là trung điểm của AB và AE. Tính diện tích thiết diện tạo bởi khối bát đó với mặt phẳng (OMN) ?
Cho hình lập phương (H). Gọi (H') là hình bát diện đều có các đỉnh là tâm các mặt của (H). Tính tỉ số diện tích toàn phần của (H) và (H') ?
Cho một bát diện đều. Hãy chỉ ra một mặt phẳng đối xứng, một tâm đối xứng và một trục đối xứng của nó ?
một khối lập phương lớn được tạo bởi 27 khối lập phương đơn vị.Một mặt phẳng vuông góc với đường chéo của khối lập phương lớn tại trung điểm của nó.Mặt phẳng này cắt ngang(không đi qua đỉnh)của bao nhiêu khối lập phương đơn vị
Cho tứ diện đều ABCD Cạnh a M là trung điểm của BC tính cos(AB,DM)
Cho ba đoạn thẳng bằng nhau, đôi một vuông góc với nhau và cắt nhau tại trung điểm của chúng. Chứng minh rằng các đầu mút của ba đoạn thẳng ấy là các đỉnh của một hình bát diện đều ?
Cho hình bát diện đều ABCDEF (h.1.24)
Chứng minh rằng :
a) Các đoạn thẳng AF, BD và CE đôi một vuông góc với nhau và cắt nhau tại trung điểm mỗi đường
b) ABFD, AEFC và BCDE là những hình vuông
Cho hình lập phương abcd.a'b'c'd' cạnh a. Điểm E là trung điểm của cạnh C'D'. Hai điểm M và N lần lượt thay đổi trên hai cạnh BC và CC'. Giá trị nhỏ nhất của tổng AM+ MN+ NE
