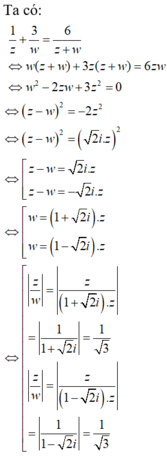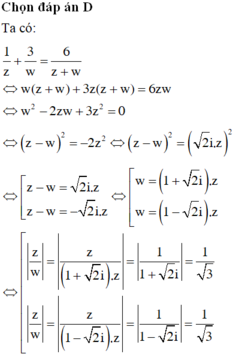Biết số thực khác 0 thỏa mãn
Khi đó

Những câu hỏi liên quan
Biết số thực a khác 0 thỏa mãn: 9(a+1/36a)^2-6(a+1/36a)+1=0 Khi đó 1/a=
Đặt \(t=a+\frac{1}{36a}\)
Ta có : \(9t^2-6t+1=0\)
\(\Leftrightarrow\left(3t-1\right)^2=0\)\(\Leftrightarrow t=\frac{1}{3}\)
\(\Leftrightarrow a+\frac{1}{36a}=\frac{1}{3}\)
\(\Leftrightarrow\frac{36a^2+1}{36a}=\frac{1}{3}\)
\(\Leftrightarrow36a^2+1=12a\)
\(\Leftrightarrow36a^2-12a+1=0\)
\(\left(6a-1\right)^2=0\)
\(\Rightarrow a=\frac{1}{6}\)
\(\Rightarrow\frac{1}{a}=6\)
Đúng 0
Bình luận (0)
Biết các số phức z,w khác 0 thỏa mãn:
z
2
+
w
2
zw Khi đó:
A
.
z
6
w
6
B
.
z
5
w
5
C
.
...
Đọc tiếp
Biết các số phức z,w khác 0 thỏa mãn: z 2 + w 2 = zw Khi đó:
A . z 6 = w 6
B . z 5 = w 5
C . z 4 = i w 4
D . z 3 + i w 3 = 0
cho a,b là hai số thực khác khác 0 thỏa mãn a-b =ab. Khi đó giá trị của a/b +b/a - ab là bao nhiêu?
a/b+b/a-ab
=a/b+b/a-(a-b)
=a/b+b/a-a+b
=a/b-a+b/a+b
=(a-ab)/b+(b+ab/a)
=(a-a+b)/b-((b+a-b)a
=1+1
=2
Đúng 0
Bình luận (0)
vì a,b khác 0 => a.b khác 0
ta có: a/b + b/a - ab
=(a^2+b^2-a^2b^2)/ab
=[(a-b)^2+2ab-a^2b^2]/ab
=(a^2b^2+2ab-a^2b^2)/ab=2ab/ab=2 (do a-b=ab)
Đúng 0
Bình luận (0)
Biết số thực a khác 0 thỏa mãn
\(9\left(a+\frac{1}{36a}\right)^2-6\left(a+\frac{1}{36a}\right)+1=0\) . Khi đó \(\frac{1}{a}=\)
Đặt \(a+\frac{1}{36a}=x\)
pt đã cho trở thành \(9x^2-6x+1=0\)
\(\Leftrightarrow9\left(x^2-\frac{2}{3}x+\frac{1}{9}\right)=0\)
\(\Leftrightarrow9\left(x-\frac{1}{3}\right)^2=0\)
\(\Leftrightarrow x-\frac{1}{3}=0\)
\(\Leftrightarrow x=\frac{1}{3}=a+\frac{1}{36a}=\frac{36a^2+1}{36a}\)
\(\Leftrightarrow12a=36a^2+1\)
\(\Leftrightarrow36a^2-12a+1=0\)
\(\Leftrightarrow\left(6a-1\right)^2=0\)
\(\Leftrightarrow6a-1=0\)
\(\Leftrightarrow a=\frac{1}{6}\Rightarrow a=6\)
Chúc bạn học tốt !!!
Đúng 0
Bình luận (0)
Cho các số phức z, w khác 0 thỏa mãn z+w khác 0 và
1
z
+
3
w
6
z
+
w
Khi đó
z
w
bằng
Đọc tiếp
Cho các số phức z, w khác 0 thỏa mãn z+w khác 0 và 1 z + 3 w = 6 z + w Khi đó z w bằng
![]()
![]()
a.Cho a, b,c là các chữ số (a, b khác 0)thỏa mãn: a nhân bcd nhân abc bằng ababc. Khi đó abcd=
b. Cặp chữ số (a, b) khác 0 thỏa mãn: a nhân b nhân ab = bbb là
Cho các số phức z, w khác 0 thỏa mãn
z
+
w
≠
0
và
1
z
+
3
w
6
z
+
w
.
Khi đó
z
w
bằng A.
3
B.
1
3
C. ...
Đọc tiếp
Cho các số phức z, w khác 0 thỏa mãn z + w ≠ 0 và 1 z + 3 w = 6 z + w . Khi đó z w bằng
A. 3
B. 1 3
C. 3
D. 1 3
Cho a, b là hai số thực dương khác 1 thỏa mãn
a
2
3
a
4
5
và
log
b
7
5
log
b
4
3
. Khi đó khẳng định nào sau đây là đúng? A.
0
a
1...
Đọc tiếp
Cho a, b là hai số thực dương khác 1 thỏa mãn a 2 3 < a 4 5 và log b 7 5 > log b 4 3 . Khi đó khẳng định nào sau đây là đúng?
A. 0 < a < 1 , 0 < b < 1
B. a > 1 , 0 < b < 1
C. 0 < a < 1 , b > 1
D. a > 1 , b > 1
cho a,b là các số khác 0 thỏa mãn a+b=4(a-b) . khi đó a/b=
1/Cho a,b,c là các số nguyên khác 0 thỏa mãn ab - ac + bc - c2 = -1.Khi đó a/b = ?? (a phần b mà mik ko bik ghi phân số )
2/Tìm a,b nguyên khác 0 thỏa mãn a + b = ab
Xem thêm câu trả lời