cho tam giác ABC cân tại A.D nằm giữa B và C . Chứng minh AD < cạnh bên ABC

Những câu hỏi liên quan
Cho tam giác ABC cân tại A, D là điểm nằm giữa B và C. Chứng minh cạnh AD bé hơn cạnh bên của tam giác ABC
Xét tgABD và tgACD có: AB=AC(GT) BD=DC vì D là trung điểm của BC và lại có AD chung=>tgABD=ACD(c.c.c)
góc ADB=ADC HAI GÓC TG UNG VÀ LẠI CÓ ADB+ACD=180o kề bù => ADB=ACD=900
Theo dinh ly pytago tổng binh p hai cah goc vuong bg bp canh huyền vay BD hay DC nho hon AB hay AC
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, điểm D nằm giữa B và C. Chứng minh rằng độ dài AD nhỏ hơn cạnh bên của tam giác ABC.
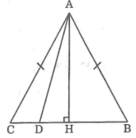
Kẻ AH ⊥ BC.
* Trường hợp H trùng với D
Ta có AH < AC (đường vuông góc ngắn hơn đường xiên)
Suy ra: AD < AC
* Trường hợp H không trùng với D
Giả sử D nằm giữa H và C.
Ta có: HD < HC
Suy ra: AD < AC (hình chiếu nhỏ hơn thì có đường xiên nhỏ hơn)
Vậy AD nhỏ hơn cạnh bên của tam giác cân ABC.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, điểm D nằm giữa B và C. Chứng minh rằng độ dài AD nhỏ hơn cạnh bên của tam giác ABC ?
Kẻ \(AH\perp BC\)
- Nếu D trùng H thì \(AD< AC\) vì \(AH< AC\) ( đường vuông góc nhỏ hơn đường xiên )
- Nếu D không trùng H, giả sử D nằm giữa H và C. Ta có: \(HD< HC\)
\(\Rightarrow AD< AC\) ( hình chiếu nhỏ hơn thì đường xiên nhỏ hơn )
Vậy AD nhỏ hơn cạnh bên của \(\Delta ABC\)
Đúng 0
Bình luận (0)
Tam giác ABC cân tại A. D nằm giữa B và C. chứng minh AD < AB
Cho tam giác ABC cân tại A, hai điểm D,E nằm trên đường thẳng BC, d nằm giữa B và C , C nằm giữa D và E. chứng minh AD<AC<AE. ai giúp em với ạ
Xem chi tiết
góc ADB=góc DAC+góc ACD
=>góc ADB>góc ACD
=>góc ADB>góc ABD
=>AB>AD
Vì ΔABC cân tại A
nên góc ACB<90 độ
=>góc ACE>90 đô
=>AE>AC=AB
=>AD<AC<AE
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, hai điểm D,E nằm trên đường thẳng BC, d nằm giữa B và C , C nằm giữa D và E. chứng minh AD<AC<AE. ai giúp em với ạ
Xem chi tiết
góc ADB=góc DAC+góc ACD
=>góc ADB>góc ACD
=>góc ADB>góc ABD
=>AB>AD
Vì ΔABC cân tại A
nên góc ACB<90 độ
=>góc ACE>90 đô
=>AE>AC=AB
=>AD<AC<AE
Đúng 1
Bình luận (0)
cho tam giác ABC ( ABAC ) , AD là tia phân giác của góc BAC (D thuộc BC) .Trên AD lấy điểm M sao cho M nằm giữa A và Da) Chứng minh tam giác ABM tam giác ACM và chứng minh tam giác BMC cân b)Đường thẳng BM cắt cạnh AC của tam giác ABC tại E,đường thẳng CM cắt cạnh AB của tam giác ABC tại F.Chứng minh AD perpEFc) Trên tia đối của CA lấy điểm K (K khác C ), đường thẳng BF cắt tia đối của tia DA tại N.Chứng minh KN BN
Đọc tiếp
cho tam giác ABC ( AB=AC ) , AD là tia phân giác của góc BAC (D thuộc BC) .Trên AD lấy điểm M sao cho M nằm giữa A và D
a) Chứng minh tam giác ABM = tam giác ACM và chứng minh tam giác BMC cân
b)Đường thẳng BM cắt cạnh AC của tam giác ABC tại E,đường thẳng CM cắt cạnh AB của tam giác ABC tại F.Chứng minh AD \(\perp\)EF
c) Trên tia đối của CA lấy điểm K (K khác C ), đường thẳng BF cắt tia đối của tia DA tại N.Chứng minh KN > BN
Tính chu vi 1 tam giác cân có 2 cạnh = 4m và 9m
Cho tam giác ABC diểm D nằm giữa B và C. Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC
Bài 1 :
Vì tam giác đó cân
=>
Có 2 cạnh là 4mCó 2 cạnh là 9mMà theo bất đẳng thức tam giác , độ dài 1 cạnh bao nhờ cũng nhỏ hơn tổng độ dài 2 cạnh còn lại
=> Tam giác đó có 2 cạnh bằng 9m .
Chu vi tam giác đó là :
9 + 9 + 4 = 22 ( m)
Đáp số : 22m
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A trên cạnh BC lấy hai điển D vàE ,BD=CE ,CD nằm giữa B và E
a) chứng minh hai tam giác ADB và tam giác AEC bằng nhuau
b)c/minh DH=EI
c)c/minh HI//BC
Xem chi tiết
đề của mk có thêm câu d) mk cho nếu cần thì bn lấy nhá
a, Vì △ABC cân tại A => AB = AC và ABC = ACB
Xét △ABD và △ACE
Có: AB = AC (cmt)
ABD = ACE (cmt)
BD = CE(gt)
=> △ABD = △ACE (c.g.c)
b, Xét △AHD vuông tại H và △AIE vuông tại I
Có: AD = AE (△ABD = △ACE)
HAD = IAE (△ABD = △ACE)
=> △AHD = △AIE (ch-gn)
=> HD = IE (2 cạnh tương ứng)
c, Xét △AHI có: AH = AI (△AHD = △AIE) => △AHI cân tại A => AHI = (180o - HAI) : 2 (1)
Vì △ABC cân tại A => ABC = (180o - BAC) : 2 (2)
Từ (1) và (2) => AHI = ABC
Mà 2 góc này nằm ở vị trí đồng vị
=> HI // BC (dhnb)
d, Gọi { O } = HD ![]() ∩ EI
∩ EI
Xét △BAM và △CAM
Có: AB = AC (cmt)
MB = MC (gt)
AM là cạnh chung
=> △BAM = △CAM (c.c.c)
=> BAM = CAM (2 góc tương ứng)
Mà AM nằm giữa AB, AC
=> AM là phân giác của BAC
Xét △HAO vuông tại H và △IAO vuông tại I
Có: AH = AI (cmt)
AO là cạnh chung
=> △HAO = △IAO (ch-cgv)
=> HAO = IAO (2 góc tương ứng)
=> AO là phân giác của BAC
Mà AM là phân giác của BAC
=> AO ≡ AM
=> 3 điểm A, M, O thẳng hàng
=> Ba đường thẳng AM, DH, EI cắt nhau tại một điểm.
a, Vì △ABC cân tại A => AB = AC và ABC = ACB
Xét △ABD và △ACE
Có: AB = AC (cmt)
ABD = ACE (cmt)
BD = CE(gt)
=> △ABD = △ACE (c.g.c)
b, Xét △AHD vuông tại H và △AIE vuông tại I
Có: AD = AE (△ABD = △ACE)
HAD = IAE (△ABD = △ACE)
=> △AHD = △AIE (ch-gn)
=> HD = IE (2 cạnh tương ứng)
c, Xét △AHI có: AH = AI (△AHD = △AIE) => △AHI cân tại A => AHI = (180o - HAI) : 2 (1)
Vì △ABC cân tại A => ABC = (180o - BAC) : 2 (2)
Từ (1) và (2) => AHI = ABC
Mà 2 góc này nằm ở vị trí đồng vị
=> HI // BC (dhnb)
d, Gọi { O } = HD ![]() ∩ EI
∩ EI
Xét △BAM và △CAM
Có: AB = AC (cmt)
MB = MC (gt)
AM là cạnh chung
=> △BAM = △CAM (c.c.c)
=> BAM = CAM (2 góc tương ứng)
Mà AM nằm giữa AB, AC
=> AM là phân giác của BAC
Xét △HAO vuông tại H và △IAO vuông tại I
Có: AH = AI (cmt)
AO là cạnh chung
=> △HAO = △IAO (ch-cgv)
=> HAO = IAO (2 góc tương ứng)
=> AO là phân giác của BAC
Mà AM là phân giác của BAC
=> AO ≡ AM
=> 3 điểm A, M, O thẳng hàng
=> Ba đường thẳng AM, DH, EI cắt nhau tại một điểm.
Cho tam giác ABC có góc A = 120 độ, đường phân giác AD (D thuộc BC). Vẽ DE vuông góc với AB, DF vuông góc với AC. a)tam giác DEF là tam giác gì?. b) Lấy K nằm giữa E và B, lấy I nằm giữa F và C sao cho EK = FI. Chứng minh tam giác DKI cân tại D. c) Từ C kẻ đường thẳng song song với AD cắt AB tại M. Chứng minh tam giác AMC đều. d) Tính DF biết AD = 4 cm
https://lazi.vn/edu/exercise/cho-tam-giac-abc-co-goc-a-120-do-duong-phan-giac-ad-d-thuoc-bc-ve-de-vuong-goc-voi-ab-df-vuong-goc
a) ΔAED=ΔAFDΔAED=ΔAFD(ch-gn)nên DE=DF.(hai cạnh tương ứng)
Mặt khác dễ dàng chứng minh được EDFˆ=60o
Vì vậy tam giác DEF là tam giác đều
b)ΔEDK=ΔFDT(hai cạnh góc vuông)
nen DK=DI(hai cạnh tương ứng).Do đó Tam giác DIK cân ở D
c) AD là tia phân giác của góc BAC nên DAB^=DAC^=1/2BAC^=60o
AD//MC(gt),do đó AMCˆ=DABˆ=60o(hai góc nằm trong vị trí đồng vị)
AMC^=CAD^=60o(hai góc nằm trong vị trí sole trong)
Tam giác AMC có hai góc bằng nhau và khoảng 60o nên là tam giác đều
d)Ta có AF=AC-FC=CM-FC=m-n.




















