a: Khi m=-1 thì hệ phương trình sẽ trở thành:

\(\left\{{}\begin{matrix}-x+y-3=3\\x-y-2\cdot\left(-1\right)+1=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-x+y=6\\x-y=-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}0x=3\left(vôlý\right)\\x-y=-3\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\varnothing\)

b: \(\left\{{}\begin{matrix}mx+y-3=3\\x+my-2m+1=0\end{matrix}\right.\)(1)

=>\(\left\{{}\begin{matrix}mx+y=6\\x+my=2m-1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=6-mx\\x+m\left(6-mx\right)=2m-1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x+6m-m^2x=2m-1\\y=6-mx\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x\left(1-m^2\right)=-4m-1\\y=6-mx\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x\left(m^2-1\right)=4m+1\\y=6-mx\end{matrix}\right.\)

TH1: m=1

Hệ phương trình (1) sẽ trở thành: 

\(\left\{{}\begin{matrix}x\cdot0=4\cdot1+1=5\\y=6-mx\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\varnothing\)

=>Loại

TH2: m=-1

Hệ phương trình (1) sẽ trở thành:

\(\left\{{}\begin{matrix}x\cdot0=-4+1=-3\\y=6-mx\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\varnothing\)

=>Loại

Th3: \(m\notin\left\{1;-1\right\}\)

Hệ phương trình (1) sẽ tương đương với \(\left\{{}\begin{matrix}x=\dfrac{4m+1}{m^2-1}\\y=6-mx=\dfrac{6\left(m^2-1\right)-m\left(4m+1\right)}{m^2-1}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{4m+1}{m^2-1}\\y=\dfrac{6m^2-6-4m^2-m}{m^2-1}=\dfrac{2m^2-m-6}{m^2-1}\end{matrix}\right.\)

Để hệ có nghiệm duy nhất thì m/1<>1/m

=>\(m^2\ne1\)

=>\(m\notin\left\{1;-1\right\}\)

Để x nguyên thì \(4m+1⋮m^2-1\)

=>\(\left(4m+1\right)\left(4m-1\right)⋮m^2-1\)

=>\(16m^2-1⋮m^2-1\)

=>\(16m^2-16+15⋮m^2-1\)

=>\(m^2-1\inƯ\left(15\right)\)

=>\(m^2-1\in\left\{1;-1;3;-3;5;-5;15;-15\right\}\)

=>\(m^2\in\left\{2;0;4;6;16\right\}\)

=>\(m\in\left\{\sqrt{2};-\sqrt{2};0;2;-2;\sqrt{6};-\sqrt{6};4;-4\right\}\)

mà m nguyên

nên \(m\in\left\{0;2;4;-2;-4\right\}\left(2\right)\)

Để y nguyên thì \(2m^2-m-6⋮m^2-1\)

=>\(2m^2-2-m-4⋮m^2-1\)

=>\(m+4⋮m^2-1\)

=>\(\left(m+4\right)\left(m-4\right)⋮m^2-1\)

=>\(m^2-16⋮m^2-1\)

=>\(m^2-1-15⋮m^2-1\)

=>\(m^2-1\inƯ\left(-15\right)\)

=>\(m^2-1\in\left\{1;-1;3;-3;5;-5;15;-15\right\}\)

=>\(m^2\in\left\{2;0;4;6;16\right\}\)

=>\(m\in\left\{\sqrt{2};-\sqrt{2};0;2;-2;\sqrt{6};-\sqrt{6};4;-4\right\}\)

mà m nguyên

nên \(m\in\left\{0;2;4;-2;-4\right\}\left(3\right)\)

Từ (2),(3) suy ra \(m\in\left\{0;2;4;-2;-4\right\}\)

Thử lại, ta sẽ thấy m=4;m=-2 không thỏa mãn x nguyên; m=4;m=-2 không thỏa mãn y nguyên

=>\(m\in\left\{0;2;-4\right\}\)

Đáp án C

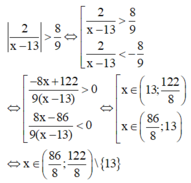
Do đó; số các nghiệm nguyên của x là 11;12;14;15

a) 

\(\Rightarrow\left(x,y\right)=\left(4;10\right)\)

Đáp án A

Ta có:  log 1 2 x 2 − 1 > − 3 ⇔ x 2 − 1 < 1 2 − 3 ⇔ 0 < x 2 − 1 < 8 ⇔ 1 < x 2 < 9.

 Vì x ∈ ℤ ⇒ x 2 = 4 ⇔ x = ± 2.  

Đáp án A

Điều kiện:  x 2 2 x − 1 > 0 ⇔ x ≠ 0 2 x − 1 > 0 ⇔ x > 1 2 .

log 4 x 2 2 x − 1 ≤ 1 2 ⇔ 1 2 log 2 x 2 2 x − 1 ≤ 1 2 ⇔ x 2 2 x − 1 ≤ 2 ⇔ x 2 ≤ 2 2 x − 1 ⇔ x 2 − 4 x + 2 ≤ 0 ⇔ 2 − 2 ≤ x ≤ 2 + 2

Kết hợp điều kiện ta được  2 − 2 ≤ x ≤ 2 + 2

Bất phương trình có 3 nghiệm nguyên là 1 ; 2 ; 3 .

Cái bạn viết không phải phương trình (không có dấu = ). Bạn xem lại đề.