cho một tam giác có đường cao ha;hb;hc tỉ lệ thuận với ba số 4;5;6. Chu vi của tam giác đó là 37 cm. Độ dài cạnh nhỏ nhất của tam giác đó là

Những câu hỏi liên quan
cho tam giác abc nhọn và AB<AC có đường cao AH. Kéo dài AH thêm một đoạn HD bằng với HA. So sánh tam giác ABH bà tam giác BHD , so sánh tam giác ACH và tam giác CDH
Xét ΔABH vuông tại H và ΔDBH vuông tại H có
BH chung
AH=DH
Do đó: ΔABH=ΔDBH
Xét ΔACH vuông tại H và ΔDCH vuông tại H có
HC chung
HA=HD
Do đó: ΔACH=ΔDCH
Đúng 0
Bình luận (0)
: Cho ABC nhọn, có đường cao AH. Trên tia đối của tia HA lấy HE = HA. Chứng minh: tam giác BAE và tam giác CAE là tam giác cân.
Mình đang rất cần
Ta có BH là đường trung trực của AE nên AB=BE⇒ΔABE cân tại B
Ta có CH là đường trung trực của AE nên AC=CE⇒ΔACE cân tại C
Đúng 0
Bình luận (0)
Bài 2: Cho tam giác ABC nhọn có đường cao AH. Trên tia đối của tia HA lấy HE=HA. Chứng minh tam giác BAE và tam giác CAE cân
TA CÓ HAI ĐỌC THẲNG AE VÀ BC CẮT NHAU TẠI H VÀ CÓ MỘT GÓC BẰNG 90
\(\Rightarrow\widehat{H_1}=\widehat{H_2}=\widehat{H_3}=\widehat{H_4}=90\)
XÉT \(\Delta BAH\)VÀ\(\Delta BEH\)CÓ
BH LÀ CẠNH CHUNG
\(\widehat{H_1}=\widehat{H_2}\left(CMT\right)\)
\(AH=EH\left(GT\right)\)
\(\Rightarrow\Delta BAH=\Delta BEH\left(C-G-C\right)\)
\(\Rightarrow AB=BE\)
VẬY \(\Delta BAE\)CÂN TẠI B(ĐPCM)
XÉT \(\Delta ACH\)VÀ\(\Delta ECH\)CÓ
CH LÀ CẠNH CHUNG
\(\widehat{H_1}=\widehat{H_3}\left(CMT\right)\)
\(AH=EH\left(GT\right)\)
\(\Rightarrow\Delta ACH=\Delta ECH\left(C-G-C\right)\)
\(\Rightarrow AC=EC\)
VẬY \(\Delta CAE\)CÂN TẠI C (ĐPCM)
Cô Chi ơi! CH là đường cao đồng thời là trung tuyến chứ ạ!
tương tự với BH!
Xem thêm câu trả lời
Cho tam giác ABC với BC = a, CA = b, AB = c và ba đường cao ứng với ba cạnh lần lượt có độ dài ha,hb,hc Gọi r là khoảng cách từ giao điểm của ba đường phân giác của tam giác đến một cạnh của tam giác. Chứng minh 1/ha+1/hb+1/hc=1/r
Cho Tam giác ABC nhọn và AB , AC có đường cao AH . Kéo dài AH thêm một đoạn HD bằng với HA . So sanh Tam giác ABH và Tam giác BHD , So sánh Tam giác ACH và Tam giác CDH
Cho tam giác ABC có b 7; c 5, cosA 3/5. Đường cao ha của tam giác ABC là A. B. 6. C. D.
Đọc tiếp
Cho tam giác ABC có b = 7; c = 5, cosA = 3/5. Đường cao ha của tam giác ABC là
A. ![]()
B. 6.
C. ![]()
D. ![]()
Chọn A.
Áp dụng định lí cosin trong tam giác ta có:
a2 = b2 + c2 = 2bc.cosA = 72 + 52 - 2.7.5.3/5 = 32
Nên ![]()
Mặt khác: sin2A + cos2A = 1 nên sin2A = 1 - cos2A = 16/25
Mà sinA > 0 nên sinA = 4/5
Mà: 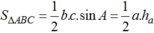
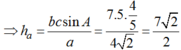
Đúng 1
Bình luận (0)
Cho tam giác ABC có góc B,C đều là góc nhọn;AH là đường cao .Nếu kéo dài HA về phía A một đoạn AM=3cm thì dc tam giác MBC có S hơn S tam giác là 18cm2.Tính BC
cho tam giác ABC có các đường phân giác cắt nhau tại N cho ha, hb,hc là đường cao gọi r là khoảng cách từ N đến cạnh tam giác. chứng minh rằng 1/ha+1/hb+1/hc=1/r
2S(ABC)=ha.a=hb.b=hc.c suy ra 1/ha+1/hb+1/hc=a/2S+b/2S+c/2S=1/2S .(a+b+c)=1/r(a+b+c) .(a+b+c) =1/r (đpcm) (vì 2S=r(a+b+c))
Đúng 0
Bình luận (1)
Cho Tam giác ABC nhọn và AB , AC có đường cao AH . Kéo dài AH thêm một đoạn HD bằng với HA . So sanh Tam giác ABH và Tam giác BHD , So sánh Tam giác ACH và Tam giác CDH'
Giair giúp với huhuhuhuhu
cho tam giác ABC nhọn và AB < AC có đường cao AH kéo dài AH thêm một đoạn HD=HA so sánh
1/ tam giác ABH và tam giác BHD
2/ tam giác ACH và tam giác CDH


















