AB = 13 cm, BC = 21 cm.

Từ đó, chu vi của tam giác ABC là 54 cm.

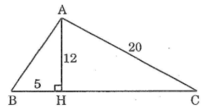
∆AHB có ∠(AHB) =90°

Theo định lý pitago, ta có:

AB2=AH2+HB2

= 122+52=169

Vậy AB = 13 cm

∆AHC có ∠(AHC) =90o

Theo định lý pitago, ta có:

AC2=AH2+HC2

HC2=AC2-AH2=202-122=400-144=256

Vậy HC = 16cm

Ta có: BC = BH + HC = 5 +16 = 21cm

Chu vi tam giác ABC là: AB + AC + BC = 13 + 20 + 21 = 54cm

Xét tam giác AHC vuông tại H có:

                AC² = HC² + AH² (định lý Pytago)

Thay số:   7.5² = HC² + 4.5²

<=> HC² = 7.5² - 4.5²

<=> HC² = 56,25 - 20,25  = 36 = 6 (cm)

Ta có: BC = BH + HC 

Thay số: BC = 1,875 + 6 = 7,875 (cm)

Xét tam giác AHB vuông tại H có:

               AB² = BH² + AH² (định lý Pytago)

Thay số: AB² = 1,875² + 4,5 ²

<=> AB² = \(\dfrac{225}{64}\) + \(\dfrac{81}{4}\) = \(\dfrac{1521}{64}\)

<=> AB = 4,875  (cm)

Chu vi tam giác ABC là: AB + AC + BC =  4,875 + 7,5 + 7,875

                                                               =    20,25  (cm)

Xét \(\Delta ABH\) có AH \(\perp\) BH , theo định lí Pytago ta có :

      AB²    =    AH²  +  BH² 

=>AB²      =   4.5²  +  1.875²

=>AB²      =   23.765625.......

=>AB       =  4.875 (cm)

Có AH \(\perp\) BC, theo định lí Pytago ta có :

     HC²  =  AH² +  AC²

=> HC²  = 76.5

=> HC   = 8.746427842 \(\approx\) 8.8 (cm)

=> BC = 10.675 (cm)

Chu vi \(\Delta ABC\) là : AC   +   BC   +   AB  =  23.05 (cm)

(tự vẽ hinh)

* Do AH vuông góc vs BC(gt)

=> Tam giác AHC và tam giác AHC là tam giác vuông tại H

* Tam giác vuông AHC có:

AC^2=AH^2+HC^2(ĐL py-ta-go)

20^2=12^2+HC^2

400=144+HC^2

HC^2=400-144

HC^2=256

HC^2=16^2(vì HC>0)

=>HC=16 cm

* Tam giác AHB có:

AB^2=AH^2+HB^2(DL py-ta-go)

AB^2=12^2+5^2

AB^2=144+25

AB^2=169

AB^2=13^2(vì AB>0)

=>AB=13 cm

*Ta có:

BH+HC=BC(AH vuống góc với BC tại H)

5+16=BC

=>BC=21cm

*Chu vi tam giác ABC:

AB+BC+AC=13+21+20=53cm

* Tam giác AHB và tam giác AHC là tam giác vuông trong vì:

AH vuông góc với BC tại H

AH cát BC tại hH tạo thành 2 tam giác vuông trong tam giác ABC

Áp dụng định lí Pythagoras vào △ABH, ta có :

        AB² = AH² + BH²

\(\Rightarrow\)20² = AH² + 16²

\(\Rightarrow\)AH²= 144

\(\Rightarrow\)AH  = 12

Áp dụng định lí Pythagoras vào △AHC, ta có :

         AC² = AH² + HC²

\(\Rightarrow\)AC² = 12² + 5²

\(\Rightarrow\)AC² = 169

\(\Rightarrow\)AC   = 13

Vậy AH = 12 cm

       AC = 13 cm

Hình bn tự vẽ nhá :) 

a,  +,  \(\Delta\) vuông AHC có : 

AC² = AH² + HC² ( Định lí py - ta - go ) 

20² cm = 12² cm + HC² 

400 cm = 144 cm + HC² 

=> HC²  = 256

    HC = 16 cm 

Ta có : BH + HC = BC 

            5 + 16 = BC 

=> BC = 21 cm 

+,     \(\Delta\) vuông AHB : 

AB² = AH² + BH² 

AB² = 12² cm + 5² cm

AB² = 144 cm + 25 cm 

AB² = 169

AB = 13 cm

=>  Chu vi \(\Delta\) ABC :  20 + 13 + 21 = 54 

b,   Diện tích \(\Delta\) ABC  : 

   \(\frac{1}{2}.21.12=126\) ( cm² ) 

Xét \(\Delta\)AHC vuông tại H:

=> AC² = HA² + HC²

HC² = AC² - HA²

HC² = 20² - 12² = 256

HC = \(\sqrt{256}\) = 16 (cm)

BC = BH + HC

BC = 5 + 16 = 21 (cm)

Xét \(\Delta\)AHB vuông tại H

=> AB² = HA² + HB²

AB² = 12² + 5²

AB² = 144 + 25 = 169

AB = \(\sqrt{169}\) = 13 (cm)

Chu vi của \(\Delta\)ABC là:

AC + CB + BA = 20 + 21 + 13

= 54 (cm)

Vậy chu vi của \(\Delta\)ABC là 54 cm.

Xét AHC vuông tại H:

=> AC2 = HA2 + HC2

HC2 = AC2 - HA2

HC2 = 202 - 122 = 256

HC = = 16 (cm)

BC = BH + HC

BC = 5 + 16 = 21 (cm)

Xét AHB vuông tại H

=> AB2 = HA2 + HB2

AB2 = 122 + 52

AB2 = 144 + 25 = 169

AB = = 13 (cm)

Chu vi của ABC là:

AC + CB + BA = 20 + 21 + 13

= 54 (cm)

Vậy chu vi của ABC là 54 cm.