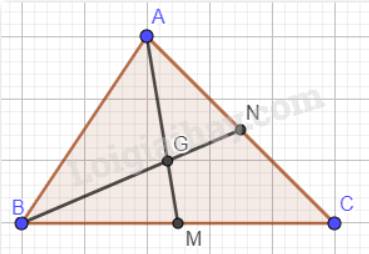
hai đường trung tuyến AM và BN của tam giac abc cắt nhau ở G. Tinh Sabc biết Sabg=336 cm2

Những câu hỏi liên quan
Hai đường trung tuyến AM và BN của tam giác ABC cắt nhau tại G.Tính diện tích tam giác AGB biết diện tích tam giác AGB bằng 336 cm
Bài 12. Cho tam giác ABC, hai đường trung tuyến AM và BN cắt nhau tại G. Đường thẳng qua C và song song với AM cắt tia BN tại D. Chứng minh rằng hai điểm B và D đối xứng qua G.
Xét ΔANG và ΔCND có
\(\widehat{GAN}=\widehat{DCN}\)
NA=NC
\(\widehat{ANG}=\widehat{CND}\)
Do đó: ΔANG=ΔCND
Suy ra: NG=ND
Xét ΔBAC có
BN là đường trung tuyến ứng với cạnh huyền AC
AM là đường trung tuyến ứng với cạnh huyền BC
BN cắt AM tại G
Do đó: G là trọng tâm của ΔBAC
Suy ra: \(BG=\dfrac{2}{3}BN\)
\(\Leftrightarrow NG=ND=\dfrac{1}{3}BN\)
\(\Leftrightarrow BG=GD\)
hay B và D đối xứng nhau qua G
Đúng 0
Bình luận (0)
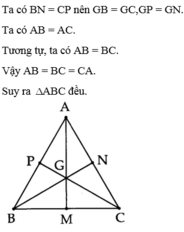
Cho tam giác ABC có ba đường trung tuyến AM, BN, CP cắt nhau tại G.
Biết AM = BN = CP. Chứng mình tam giác ABC đều.
Cho tam giác ABC có trung tuyến AM và BN cắt nhau tại G.Cm:
a)SAMB=1/2 SABC
b)SGBM=1/2 SABC
Cho tam giác ABC có các đường trung tuyến AM, BN, CP trọng tâm G. Gọi K là trung điểm của GB
Chứng minh rằng các cạnh của tam giác GMK bằng 1/3 các trung tuyến tam giác ABC
Nêu cách dựng tam giac ABC khi biết đọ dài 3 đường trung tuyến AM, BN, CP
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Khi đó
A.\(AM = 2GM\). B.\(AM = 2AG\). C.\(GA = 3GM\). D.\(GA = 2GM\).
Cho △ABC, hai trung tuyến AM, BN cắt nhau tại G. SAGB = 336 cm2. Tính SABC
Lời giải:
Vì $G$ là giao điểm của hai đường trung tuyến nên $G$ là trọng tâm. Theo tính chất trọng tâm và đường trung tuyến thì \(AG=\frac{2}{3}AM\)
Khi đó:
\(\frac{S_{ABG}}{S_{ABM}}=\frac{AG}{AM}=\frac{2}{3}(1)\)
Mà: \(\frac{S_{ABM}}{S_{ABC}}=\frac{BM}{BC}=\frac{1}{2}(2)\)
Từ \((1);(2)\Rightarrow \frac{S_{ABG}}{S_{ABC}}=\frac{2}{3}.\frac{1}{2}=\frac{1}{3}\)
\(\Rightarrow S_{ABC}=3S_{ABG}=3.336=1008(cm^2)\)
Đúng 0
Bình luận (0)
tam giac ABC có 2 đường trung tuyến AM và BN vuông góc với nhau. Tính diện tích tam giác ABC theo AM và BN
Cho tam giác ABC câb tại A có AB=5cm, BC=8cm. Hai đường trung tuyến AM,BN của tam giác ABC cắt nhau tại G. Tính AG