Xét ∆AHB và ∆ CKD có:HB = KD (= 1 ô)AHBˆ = CKDˆAH = CK (= 3 ô)=> ∆AHB = ∆CKD(c.g.c)=> AB = CD (cạnh tương ứng)Chứng minh tương tự ta đươc: ∆ CEB = ∆ AFD (c.g.c)suy ra BC=AD.b) Xét ∆ABD và ∆CDB có:AB = CD (cmt)BC = AD (cmt)BD chung.=> ∆ABD = ∆CDB (c.c .c)=> ABDˆ = CDBˆMà hai góc này ở vị trí so le trongVậy AB // CD (đpcm)

chả bt có khớp ko chứ lười đọc quá

đây bạn nhé

BC=2cm

AD²=8²+6²= 100 = 10cm

AB²=10²+2²= Xấp xỉ của 10cm

CD²=4²+4²= 32 = xấp xỉ của 6cm

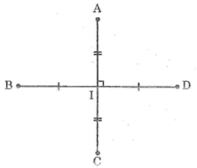
Gọi I là giao điểm của AC và BD

Ta có: I là trung điểm AC nên IA = IC = AC/2=6cm

Vì I là trung điểm của BD nên IB = ID = BD/2=8cm

Áp dụng định lí pitago vào tam giác vuông AIB ta có:

AB2=IA2+IB2

AB2=62+82=36+64=100

Vậy AB = 10 cm

Mặt khác: ΔIAB=ΔIAD=ΔICB=ΔICD(c.g.c)

Suy ra: AD = BC = CD = AB = 10cm

AB=21/(3+4)x3=9 cm

AC=21-9=12cm

Tự kẻ hình bạn nhé =)))

Áp dụng định lí Pitago vào tam giác ABC , có

AB^2+AC^2=BC^2

=>thay số vào, tính được BC=15cm

Áp dụng hệ thức giữa cạnh và đường cao trong tg vuông, có:

AB^2=BHxBC

=>BH=81/15=5.4cm

=>CH=15-5.4=9.6cm

AH^2=BHxCH=5.4x9.6=51.84cm

a: AC=căn 5^2-3^2=4cm

AH=3*4/5=2,4cm

BH=3^2/5=1,8cm

CH=5-1,8=3,2cm

b: \(BH=\sqrt{60^2:144}=5\left(cm\right)\)

BC=144+5=149cm

\(AB=\sqrt{5\cdot149}=\sqrt{745}\left(cm\right)\)

\(AC=\sqrt{144\cdot149}=12\sqrt{149}\left(cm\right)\)

c: \(HC=\sqrt{AC^2-AH^2}=\dfrac{144}{13}\left(cm\right)\)

\(BH=\dfrac{AH^2}{HC}=\dfrac{25}{13}cm\)

BC=BH+CH=13(cm)

AB=căn 13^2-12^2=5cm

a

Áo dụng đl pytago vào tam giác ABC vuông tại A:

\(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)

Theo hệ thức lượng vào tam giác ABC vuông tại A có đường cao AH:

\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{3^2}{5}=1,8\left(cm\right)\)

\(CH=BC-BH=5-1,8=3,2\left(cm\right)\)

\(AH.BC=AB.AC\Rightarrow AH=\dfrac{3.4}{5}=2,4\left(cm\right)\)

b

Áp dụng đl pytago vào tam giác AHC vuông tại H có:

\(AC=\sqrt{AH^2+HC^2}=\sqrt{60^2+144^2}=156\left(cm\right)\)

Theo hệ thức lượng vào tam giác ABC vuông tại A, đường cao AH có:

\(AC^2=HC.BC\Rightarrow BC=\dfrac{AC^2}{HC}=\dfrac{156^2}{144}=169\left(cm\right)\)

\(BH=BC-HC=169-144=25\left(cm\right)\)

\(AB^2=BH.BC\Rightarrow AB=\sqrt{25.169}=65\left(cm\right)\)

c

Áp dụng đl pytago vào tam giác AHC vuông tại H:

\(HC=\sqrt{AC^2-AH^2}=\sqrt{12^2-\left(\dfrac{60}{13}\right)^2}=\dfrac{144}{13}\approx11,08\left(cm\right)\)

Theo hệ thức lượng vào tam giác ABC đường cao AH có:

\(AH^2=HB.HC\Rightarrow HB=\dfrac{AH^2}{HC}=\dfrac{\left(\dfrac{60}{13}\right)^2}{\dfrac{144}{13}}=\dfrac{25}{13}\approx1,92\left(cm\right)\)

\(BC=HB+HC=\dfrac{25}{13}+\dfrac{144}{13}=13\left(cm\right)\)

\(AB^2=HB.BC\Rightarrow AB=\sqrt{HB.HC}=\sqrt{\dfrac{144}{13}.\dfrac{25}{13}}=\dfrac{60}{13}\approx4,62\left(cm\right)\)

việt jack hoặc qanda đi chị

Gọi I là giao điểm của AC và BD

Ta có: I là trung điểm AC nên IA = IC = AC/2=6cm

Vì I là trung điểm của BD nên IB = ID = BD/2=8cm

Áp dụng định lí pitago vào tam giác vuông AIB ta có:

AB2=IA2+IB2

AB2=62+82=36+64=100

Vậy AB = 10 cm

Mặt khác: ΔIAB=ΔIAD=ΔICB=ΔICD(c.g.c)

Suy ra: AD = BC = CD = AB = 10cm