Cho hình vuông ABCD. Tính cos góc MAN biết rằng M, N theo thứ tự là trung điểm của BC, C

Những câu hỏi liên quan
cho hình vuông ABCD . biết M và N theo thứ tự là trung điểm của BC và CD biết tam giác AMD cân tại M . tính COS góc MAN
Cho hình vuông ABCD. Gọi M và N là trung điểm của BC và DC. Tính cos góc MAN
cos(300) =\(\frac{\sqrt{3}}{2}\)
lik-e nha
Đúng 1
Bình luận (0)
Cho hình vuông ABCD . gọi M ,N lần lượt là trung điểm của BC và CD. Tính cos góc MAN
Vì \(\tan MAB=\frac{MB}{AB}=\frac{1}{2}\Rightarrow\widehat{MAB}=26,5°\)Tương tự có \(\widehat{NAD}=26,5°\)
\(\Rightarrow\widehat{MAN}=37°\Rightarrow\cos MAN=\cos37\approx0,79\)
Cho hình vuông ABCD. Tính cos MAN biết rằng M, N theo thứ tự là trug điểm của BC, CD.
Đặt AB=BC=CD=AD=2a
=>NC=MC=BM=DN=a
\(NM=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(AM=\sqrt{\left(2a\right)^2+a^2}=a\sqrt{5}\)
\(AN=\sqrt{\left(2a\right)^2+a^2}=a\sqrt{5}\)
Xét ΔMAN có \(cosMAN=\dfrac{AM^2+AN^2-MN^2}{2\cdot AM\cdot AN}=\dfrac{5a^2+5a^2-2a^2}{2\cdot a\sqrt{5}\cdot a\sqrt{5}}\)
\(=\dfrac{8a^2}{10a^2}=\dfrac{4}{5}\)
Đúng 0
Bình luận (0)
Chi hình vuông ABCD biết M và N là trung tuyến của BC và CD. Biết tam giác ADM cân tại M . Tính Cos của góc MAN
Cho hình vuông ABCD có cạnh bằng 2a. Gọi M, N lần lượt là trung điểm của BC, CD. Tính cos(MAN).
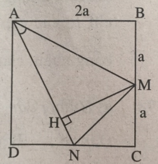
Kẻ đường cao MH của tam giác cân AMN. Ta có sin ∠ (NAM) = HM/AM và diện tích tam giác AMN là S A M N = 1/2AN.MH = 1/2AN.AM.sin(NAM) = 1/2 A N 2 .sin(NAM) = 1/2( A D 2 + D N 2 ). sin(NAM) = ( 5 a 2 )/2 sin(NAM).
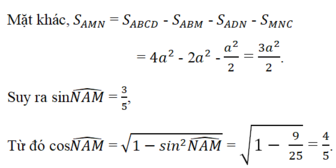
Đúng 1
Bình luận (0)
Cho hình vuông ABCD. Gọi E, F theo thứ tự là trung điểm của AB, BC. Chứng minh rằng CE vuông góc với DF.
Xét ∆ BEC và ∆ CFD , ta có: BE = CF (gt)
∠ B = ∠ C = 90 0
BC = CD (gt)
Suy ra: ∆ BEC = ∆ CFD (c.g.c) ⇒ ∠C1 = ∠D1
Lại có: ∠ C 1 + ∠ C 2 = 90 0
Suy ra: ∠ D 1 + ∠ C 2 = 90 0
Trong ΔDCM có ∠ D 1 + ∠ C 2 = 90 0
Suy ra: ∠ (DMC) = 90 0
Vậy CE ⊥ DF
Đúng 0
Bình luận (0)
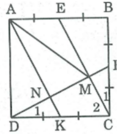
Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Biết AC = 6cm, BD = 8cm. Gọi M, N, P, Q theo thứ tự là trung điểm các cạnh AB, BC, CD, DA. Gọi X, Y, Z, T theo thứ tự là trung điểm các cạnh MN, NP, PQ, QM. Chứng minh rằng MNPQ là hình chữ nhật.
Trong △ ABD ta có:
M là trung điểm của AB
Q là trung điểm của AD nên MQ là đường trung bình của △ ABD.
⇒ MQ // BD và MQ = 1/2 BD (tính chất đường trung bình của tam giác) (1)
Trong △ CBD ta có:
N là trung điểm của BC
P là trung điểm của CD
nên NP là đường trung bình của △ CBD
⇒ NP // BD và NP = 1/2 BD (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: MQ // NP và MQ = NP nên tứ giác MNPQ là hình bình hành
AC ⊥ BD (gt)
MQ // BD
Suy ra: AC ⊥ MQ
Trong △ ABC có MN là đường trung bình ⇒ MN // AC
Suy ra: MN ⊥ MQ hay (NMQ) = 90 0
Vậy tứ giác MNPQ là hình chữ nhật.
Đúng 0
Bình luận (0)
Cho hình vuông ABCD. Gọi M và N theo thứ tự là trung điểm của AB và BC.
a) Chứng minh rằng CM = DN
b) Chứng minh rằng CM vuông góc với DN.
c) Gọi E là giao điểm của CM và DN. Chứng minh rằng AE = BC.
p.s: mọi người giúp em câu c ạ. Em cảm ơn.












