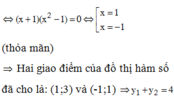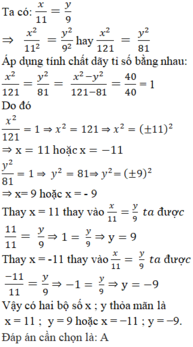Tìm x và y biết rằng x8=y9x8=y9 , x2−y2=−68x2−y2=−68 , x và y là những số dương.

Những câu hỏi liên quan
Biết rằng đồ thị hàm số
y
2
x
+
1
x
và đồ thị hàm số
y
x
2
+
x
+
1
có hai điểm chung, kí hiệu
x...
Đọc tiếp
Biết rằng đồ thị hàm số y = 2 x + 1 x và đồ thị hàm số y = x 2 + x + 1 có hai điểm chung, kí hiệu x 1 , y 1 , x 2 , y 2 là tọa độ hai điểm đó. Tìm y 1 + y 2 .
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]()
1,Cho biết y tỷ lệ thuật với x theo hệ số tỷ lệ là - 0,4 và x tỷ lệ thuận với z theo hệ số tỷ lệ là 10. Chứng tỏ rằng y tỷ lệ thuận với z và tìm hệ số tỷ lệ?2, Cho biết x và y là 2 đại lượng tỷ lệ thuận , x1 và x2 là 2 giá trị khác nhau của x, y1 và y2 là 2 giá trị tương ứng của ya, Tính x1 biết y1 -3, y2 -2 , x3 -3.b, Tính x2, y2 biết x2 + y2 10 thì x12 thì x13
Đọc tiếp
1,Cho biết y tỷ lệ thuật với x theo hệ số tỷ lệ là - 0,4 và x tỷ lệ thuận với z theo hệ số tỷ lệ là 10. Chứng tỏ rằng y tỷ lệ thuận với z và tìm hệ số tỷ lệ?
2, Cho biết x và y là 2 đại lượng tỷ lệ thuận , x1 và x2 là 2 giá trị khác nhau của x, y1 và y2 là 2 giá trị tương ứng của y
a, Tính x1 biết y1 = -3, y2= -2 , x3 = -3.
b, Tính x2, y2 biết x2 + y2 = 10 thì x1=2
thì x1=3
1/ theo bài ra ta có:
y tỉ lệ thuận vs x theo hệ số tỉ lệ là -0,4
=> y = -0,4x (1)
x tỉ lệ thuận với z theo hệ số tỉ lệ là 10
=> x = 10z (2)
thay 2 vào 1 ta có:
y = -0,4. 10z
=> y = -4z
vậy y tỉ lệ thuận với z theo hệ số tỉ lệ là -4
Đúng 0
Bình luận (0)
Biết rằng đồ thị hàm số
y
2
x
+
1
x
và đồ thị hàm số
y
x
2
+
x
+
1
cắt nhau tại hai điểm, ký hiệu
x
1
;
y
1
,...
Đọc tiếp
Biết rằng đồ thị hàm số y = 2 x + 1 x và đồ thị hàm số y = x 2 + x + 1 cắt nhau tại hai điểm, ký hiệu x 1 ; y 1 , x 2 , y 2 là tọa độ hai điểm đó. Tìm y 1 + y 2
A. y 1 + y 2 = 0
B. y 1 + y 2 = 2
C. y 1 + y 2 = 6
D. y 1 + y 2 = 4
Cho x và y là hai đại lượng tỉ lệ thuận. Gọi x1;x2 là hai giá trị của x và y1,y2 là hai giá trị tương ứng của y. Biết rằng khi x1-x2=12 thì y1-y2=-3 a) Tìm hệ số tỉ lệ k của y đối với 2 và biểu diễn y theo x. b) Tính giá trị của y khi x=-2; x=4
Cho các số x, y, z dương. Chứng minh rằng x2/y2 + y2/z2 + z2/x2 ≥ x/y + y/z + z/x
Cho các số x, y, z dương. Chứng minh rằng x2/y2 + y2/z2 + z2/x2 ≥ x/y + y/z + z/x
Cho các số x, y, z dương. Chứng minh rằng x2/y2 + y2/z2 + z2/x2 ≥ x/y + y/z + z/x
Có bao nhiêu bộ số x; y thỏa mãn
x
11
y
9
và
x
2
-
y
2
40
A. 2 B. 3 C. 4 D. 1
Đọc tiếp
Có bao nhiêu bộ số x; y thỏa mãn x 11 = y 9 và x 2 - y 2 = 40
A. 2
B. 3
C. 4
D. 1
Cho biết y tỉ lệ thuận với x1 ; x2 là các giá trị của x . Y1;y2 là các giá trị tương ướng của y a) Biết x;y Tỉ lệ thuận và x1 2 ; x2 3 ; y1 1/2 . Tìm y2 ? b) Biết x;y Tỉ lệ nghịch và x1 1/2 ; y1 4 ; y2 -4 . Tìm x2 Giúp mk đi ai đúng mk tích cho
Đọc tiếp
Cho biết y tỉ lệ thuận với x1 ; x2 là các giá trị của x . Y1;y2 là các giá trị tương ướng của y
a) Biết x;y Tỉ lệ thuận và x1 = 2 ; x2 = 3 ; y1 = 1/2 . Tìm y2 ?
b) Biết x;y Tỉ lệ nghịch và x1 = 1/2 ; y1 = 4 ; y2 = -4 . Tìm x2
Giúp mk đi ai đúng mk tích cho
Lời giải:
a. Vì $x,y$ tỉ lệ thuận nên đặt $y=kx$. Ta có:
$y_1=kx_1$ hay $\frac{1}{2}=k.2\Rightarrow k=\frac{1}{4}$. Vậy $y=\frac{1}{4}x$
$y_2=kx_2=\frac{1}{4}x_2=\frac{1}{4}.3=\frac{3}{4}$
b.
Vì $x,y$ tỉ lệ nghịch nên đặt $xy=k$.
$x_1y_1=k=x_2y_2$
$\Leftrightarrow \frac{1}{2}.4=x_2.(-4)$
$\Leftrightarrow x_2=\frac{-1}{2}$
Đúng 0
Bình luận (0)
Tìm 5 giá trị của x biết 5,8>x>5,7