Các câu hỏi tương tự
Cho (C) là đồ thị của hàm số
y
x
-
3
x
+
1
Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN. A. I(-1;1) B.I(0;-3/2) C.I(0;3/2) D. I(-2;2)
Đọc tiếp
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN.
A. I(-1;1)
B.I(0;-3/2)
C.I(0;3/2)
D. I(-2;2)
Cho hàm số y x3- x2+ x 1 có đồ thị ( C) . Tiếp tuyến tại điểm N( x; y) của (C) cắt đồ thị (C) tại điểm thứ hai là M( -1; -2) . Khi đó x+ y? A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Cho hàm số y= x3- x2+ x= 1 có đồ thị ( C) . Tiếp tuyến tại điểm N( x; y) của (C) cắt đồ thị (C) tại điểm thứ hai là M( -1; -2) . Khi đó x+ y=?
A. 1
B. 2
C. 3
D. 4
Tọa độ giao điểm của đồ thị các hàm số:
y
x
2
-
2
x
-
3
x
-
2
và y x + 1 là:A. (2; 2); B. (2; -3);C(-1; 0); D....
Đọc tiếp
Tọa độ giao điểm của đồ thị các hàm số: y = x 2 - 2 x - 3 x - 2
và y = x + 1 là:
A. (2; 2); B. (2; -3);
C(-1; 0); D. (3; 1).
Tọa độ giao điểm của đồ thị các hàm số:
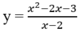
và y = x + 1 là:
A. (2; 2); B. (2; -3);
C(-1; 0); D. (3; 1).
Cho (C) là đồ thị của hàm số
y
x
-
3
x
+
1
Biết rằng chỉ có đúng hai điểm thuộc đồ thị (C) cách đều hai trục tọa độ. Gọi các điểm đó lần lượt là M và N. Tính độ dài đoạn thẳng MN. A. B. MN 3 C. D.
Đọc tiếp
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 Biết rằng chỉ có đúng hai điểm thuộc đồ thị (C) cách đều hai trục tọa độ. Gọi các điểm đó lần lượt là M và N. Tính độ dài đoạn thẳng MN.
A.![]()
B. MN = 3
C. ![]()
D. ![]()
Cho hai hàm số
f
(
x
)
a
x
3
+
b
x
2
+
c
x
-
1
2
và
g
(
x
)
d
x
2
+
e
x
+
1
(
a
,
b
,
c
,
d...
Đọc tiếp
Cho hai hàm số f ( x ) = a x 3 + b x 2 + c x - 1 2 và g ( x ) = d x 2 + e x + 1 ( a , b , c , d , e ∈ ℝ ) . Biết rằng đồ thị của hàm số y = f(x) và y = g(x) cắt nhau tại ba điểm có hoành độ lần lượt là –3; –1;1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
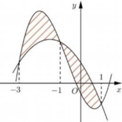
A. 9 2
B. 8
C. 4
D. 5
Cho hàm số \(y=\dfrac{1}{2}x^4-x^2+m\)(m là tham số ) có đồ thị (Cm), đường tròn (S)có phương trình \(x^2+y^2+2x+6y+1=0\) và điểm A(-1;-6).Tìm m để tồn tại tiếp tuyến với đồ thị (Cm) cắt đường tròn (S) tại hai điểm phân biệt B,C sao cho tam giác ABC có chu vi đạt giá trị lớn nhất
Trong mặt phẳng tọa độ Oxy, cho đồ thị hàm số
y
x
+
1
x
-
1
. A và B là hai điểm thay đổi trên đồ thị sao cho tiếp tuyến của đồ thị tại A và B song song với nhau. Biết rằng đường thẳng AB luôn đi qua một điểm cố định. Tọa độ của điểm đó là
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đồ thị hàm số y = x + 1 x - 1 . A và B là hai điểm thay đổi trên đồ thị sao cho tiếp tuyến của đồ thị tại A và B song song với nhau. Biết rằng đường thẳng AB luôn đi qua một điểm cố định. Tọa độ của điểm đó là
![]()
![]()
![]()
![]()
Cho (C) là đồ thị của hàm số y(x-2)/(x+1) và đường thẳng d:ymx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C) A. B. C. D.
Đọc tiếp
Cho (C) là đồ thị của hàm số y=(x-2)/(x+1) và đường thẳng d:y=mx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A.![]()
B.![]()
C.![]()
D. ![]()





