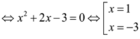Các câu hỏi tương tự
Cho (C) là đồ thị của hàm số
y
x
-
3
x
+
1
Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN. A. I(-1;1) B.I(0;-3/2) C.I(0;3/2) D. I(-2;2)
Đọc tiếp
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN.
A. I(-1;1)
B.I(0;-3/2)
C.I(0;3/2)
D. I(-2;2)
Cho hàm số
y
x
+
2
2
x
+
3
có đồ thị (C). Giả sử, đường thẳng d: ykx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác
∆
O
A
B
cân tại gốc tọa độ O. Tổng k+m có giá trị bằng: A. 1. B. 3. C. -1. D. -3.
Đọc tiếp
Cho hàm số y = x + 2 2 x + 3 có đồ thị (C). Giả sử, đường thẳng d: y=kx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác ∆ O A B cân tại gốc tọa độ O. Tổng k+m có giá trị bằng:
A. 1.
B. 3.
C. -1.
D. -3.
Tọa độ điểm M thuộc đồ thị (C) của hàm số y
x
+
3
x
-
1
cách đều hai trục tọa độ là A. B. C. D.
Đọc tiếp
Tọa độ điểm M thuộc đồ thị (C) của hàm số y = x + 3 x - 1 cách đều hai trục tọa độ là
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho đồ thị (C) của hàm số
y
x
-
3
x
+
1
Điểm M nào dưới đây thuộc đồ thị (C) và cách đều hai trục tọa độ A. B. C. D.
Đọc tiếp
Cho đồ thị (C) của hàm số y = x - 3 x + 1 Điểm M nào dưới đây thuộc đồ thị (C) và cách đều hai trục tọa độ
A.![]()
B.![]()
C.![]()
D. ![]()
Cho đồ thị (C) của hàm số
y
x
2
-
3
x
+
3
-
x
+
1
. Tìm điểm M trên đồ thị (C) sao cho M cách đều hai trục tọa độ A. B. C. D.
Đọc tiếp
Cho đồ thị (C) của hàm số y = x 2 - 3 x + 3 - x + 1 . Tìm điểm M trên đồ thị (C) sao cho M cách đều hai trục tọa độ
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số
y
x
−
1
x
+
1
có đồ thị (C), điểm M di động trên (C). Gọi d là tổng khoảng cách từ M đến hai trục tọa độ. Khi đó giá trị nhỏ nhất của d là: A.
207
250
.
B.
2
−
1.
C.
2
2
−
1....
Đọc tiếp
Cho hàm số y = x − 1 x + 1 có đồ thị (C), điểm M di động trên (C). Gọi d là tổng khoảng cách từ M đến hai trục tọa độ. Khi đó giá trị nhỏ nhất của d là:
A. 207 250 .
B. 2 − 1.
C. 2 2 − 1.
D. 2 2 − 2 .
Cho hàm số
y
x
+
2
x
+
1
có đồ thị (C). Biết rằng (C) có hai điểm A và B sao cho tiếp tuyến của (C) tại A và B cùng tạo với hai trục tọa độ một tam giác cân. Tính độ dài AB.
Đọc tiếp
Cho hàm số y = x + 2 x + 1 có đồ thị (C). Biết rằng (C) có hai điểm A và B sao cho tiếp tuyến của (C) tại A và B cùng tạo với hai trục tọa độ một tam giác cân. Tính độ dài AB.
![]()
![]()
![]()
![]()
Cho hàm số
y
x
-
1
x
+
2
có đồ thị (C) . Gọi I là giao điểm của hai tiệm cận của (C) . Xét tam giác đều ABI có hai đỉnh A; B thuộc (C) , đoạn thẳng AB có độ dài bằng A.
6
.
B.
2
3
.
C. 2. D.
2
2...
Đọc tiếp
Cho hàm số y = x - 1 x + 2 có đồ thị (C) . Gọi I là giao điểm của hai tiệm cận của (C) . Xét tam giác đều ABI có hai đỉnh A; B thuộc (C) , đoạn thẳng AB có độ dài bằng
A. 6 .
B. 2 3 .
C. 2.
D. 2 2 .
Gọi M và N là giao điểm của đồ thị hai hàm số y = x 4 - 2 x 2 + 2 và y = - x 2 + 4 . Tọa độ trung điểm I của đoạn thẳng MN là
A. (1;0)
B. (0;2)
C. (2;0)
D. (0;1)