giá trị của Ia-bI
a:4=b:7 và ab=28
Những câu hỏi liên quan
Câu 2. Giả sử x và y là hai đại lượng tỉ lệ thuận, x1; x2 là hai giá trị khác nhau của x và y1; y2 là hai giá trị tương ứng của y. Biết y1 – x1 7 và x2 – 4; y2 3, giá trị của x1; y1 là
A. x1 –28; y1 21;
B. x1 –3; y1 4;
C. x1 –4; y1 3;
D. x1 4; y1 –3.
Đọc tiếp
Câu 2. Giả sử x và y là hai đại lượng tỉ lệ thuận, x1; x2 là hai giá trị khác nhau của x và y1; y2 là hai giá trị tương ứng của y. Biết y1 – x1 = 7 và x2 = – 4; y2 = 3, giá trị của x1; y1 là
A. x1 = –28; y1 = 21;
B. x1 = –3; y1 = 4;
C. x1 = –4; y1 = 3;
D. x1 = 4; y1 = –3.
Lời giải:
Vì $x,y$ là 2 đại lượng tỉ lệ thuận nên đặt $y=ax$.
Ta có:
$y_2=ax_2$
$3=a(-4)\Rightarrow a=\frac{-3}{4}$. Vậy $y=\frac{-3}{4}x$. Thay vào điều kiện $y_1-x_1=7$ ta có:
$\frac{-3}{4}x_1-x_1=7$
$\frac{-7}{4}x_1=7$
$\Rightarrow x_1=-4$
$y_1=7+x_1=7+(-4)=3$
Đáp án C
Đúng 1
Bình luận (0)
cho a,b thuộc R sao cho ab=1 và Ia+bI đạt giá trị bé nhất. tính già trị của biểu thức A= 3a^2 - 2a + 3b^2 - 2b + 6IaI +1
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
Đúng 0
Bình luận (0)
\(A=\sqrt{28}-\sqrt{63}+\dfrac{7+\sqrt{7}}{\sqrt{7}}-\sqrt{\left(\sqrt{7}+1\right)^2}\)
\(B=\left(\dfrac{1}{\sqrt{x}+3}+\dfrac{1}{\sqrt{x}-3}\right)\dfrac{4\sqrt{x}+12}{\sqrt{x}}\) (ĐK x>0; x\(\ne9\))
a)Rút gọn A và B
b) Tìm các giá trị của x để giá trị biểu thức A lớn hơn giá trị biểu thức B
a) \(A=\sqrt{28}-\sqrt{63}+\dfrac{7+\sqrt{7}}{\sqrt{7}}-\sqrt{\left(\sqrt{7}+1\right)^2}\)
\(=2\sqrt{7}-3\sqrt{7}+\dfrac{\sqrt{7}\left(\sqrt{7}+1\right)}{\sqrt{7}}-\left|\sqrt{7}+1\right|\)
\(=-\sqrt{7}+\sqrt{7}+1-\sqrt{7}-1=-\sqrt{7}\)
\(B=\left(\dfrac{1}{\sqrt{x}+3}+\dfrac{1}{\sqrt{x}-3}\right)\dfrac{4\sqrt{x}+12}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}-3+\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{4\left(\sqrt{x}+3\right)}{\sqrt{x}}=\dfrac{2\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{4\left(\sqrt{x}+3\right)}{\sqrt{x}}\)
\(=\dfrac{8}{\sqrt{x}-3}\)
b) \(A>B\Rightarrow-\sqrt{7}>\dfrac{8}{\sqrt{x}-3}\Rightarrow\dfrac{8}{\sqrt{x}-3}+\sqrt{7}< 0\)
\(\Rightarrow\dfrac{\sqrt{7x}+8-3\sqrt{7}}{\sqrt{x}-3}< 0\)
Ta có: \(\left\{{}\begin{matrix}8=\sqrt{64}\\3\sqrt{7}=\sqrt{63}\end{matrix}\right.\Rightarrow8-3\sqrt{7}>0\Rightarrow8-3\sqrt{7}+\sqrt{7x}>0\)
\(\Rightarrow\sqrt{x}-3< 0\Rightarrow\sqrt{x}< 3\Rightarrow x< 9\Rightarrow0< x< 9\)
Đúng 2
Bình luận (0)
Xét các số phức
z
a
+
b
i
a
,
b
∈
R
thỏa mãn |z-4-3i|2. Khi |z+1-3i|+|z-1+i| đạt giá trị lớn nhất, giá trị của a – 2b bằng A. 1 B. -2 C.
-
5
D. -1
Đọc tiếp
Xét các số phức z = a + b i a , b ∈ R thỏa mãn |z-4-3i|=2. Khi |z+1-3i|+|z-1+i| đạt giá trị lớn nhất, giá trị của a – 2b bằng
A. 1
B. -2
C. - 5
D. -1
Với 
Khi đó
Dấu bằng đạt tại
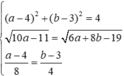
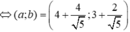
⇒ a - 2 b = - 2
Chọn đáp án B.
Mẹo trắc nghiệm: Có
Khi đó
Khi đó a-2b
Chọn đáp án B.
Đúng 0
Bình luận (0)
giá trị /a-b/ biết a:4=b:7 và a.b=28
nhờ các bạn giải giùm và nhanh tay tí nhé, đang vội
Vì \(a:4=b:7\Rightarrow\frac{a}{4}=\frac{b}{7}\left(1\right)\)
Đặt \(\frac{a}{4}=\frac{b}{7}=k\Rightarrow a=4k;b=7k\)
Ta có:a.b=4k.7k=28k2=28
Do đó:k=1;-1(2)
Từ (1) và (2) suy ra:TH1:a=4;b=7
TH2:a=-4;b=-7
Vậy TH1:|a-b|=|4-7|=3
TH2:|a-b|=|-4-(-7)|=3
Đúng 0
Bình luận (0)
Câu nào dưới đây nói về mối liên hệ của cường độ dòng điện
I
A
chạy qua đèn điôt chân không với hiệu điện thế
U
A
K
giữa anôt A và catôt K là không đúng ?A. Khi catôt K không bị nung nóng, thì
I
A
0 với mọi giá trị của
U
A...
Đọc tiếp
Câu nào dưới đây nói về mối liên hệ của cường độ dòng điện I A chạy qua đèn điôt chân không với hiệu điện thế U A K giữa anôt A và catôt K là không đúng ?
A. Khi catôt K không bị nung nóng, thì I A = 0 với mọi giá trị của U A K .
B. Khi catôt bị nung nóng ở nhiệt độ cao, thì I A ≠ 0 với mọi giá trị của U A K .
C. Khi catot bị nung nóng ở nhiệt độ cao, thì I A tăng theo mọi giá trị dương của U A K .
D. Khi catôt bị nung nóng ở nhiệt độ cao và tăng dần U A K từ 0 đến một giá trị dương Ubh thì I A sẽ tăng dần tới giá trị không đổi Ibh gọi là dòng điện bão hoà.
Xét các số phức
z
a
+
b
i
a
,
b
∈
ℝ
có modun bằng 2 và có phần ảo dương. Tính giá trị của biểu thức
S
5
a
+
b
+
2...
Đọc tiếp
Xét các số phức z = a + b i a , b ∈ ℝ có modun bằng 2 và có phần ảo dương. Tính giá trị của biểu thức S = 5 a + b + 2 2018 khi biểu thức P = 2 + z + 3 2 - z đạt giá trị lớn nhất
A. S = 1
B. S = 2 2018
C. S = 2 1009
D. S = 0
Cho a, b thuộc R sao cho ab = 1 và Ia+bI đạt giá trị nhỏ nhất. Tính giá trị của biểu thức A= 3a^2 - 2a + 3b^2 - 2b + 6IaI + 1 ( chữ I I là dấu GTTĐ nha các bạn tại mình ko biết gõ nó ở đâu)
Cho số phức
z
a
+
b
i
a
,
b
∈
ℝ
thỏa mãn đồng thời hai điều kiện
z
z
¯
-
1
-
i
và biểu thức
A
z
-...
Đọc tiếp
Cho số phức z = a + b i a , b ∈ ℝ thỏa mãn đồng thời hai điều kiện z = z ¯ - 1 - i và biểu thức A = z - 2 + 2 i + z - 3 + i đạt giá trị nhỏ nhất. Giá trị của biểu thức a+b bằng
A. -1
B. 2
C. -2
D. 1
