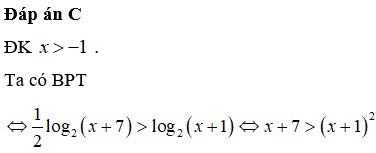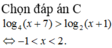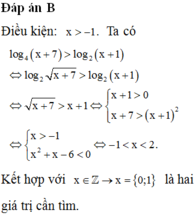log2(x) +log3(X+1) < log4(X+2) +log5(X+3)

Những câu hỏi liên quan
Biết rằng
log
2
(
log
3
(
log
4
x
)
)
log
3
(
log
4
(
log
2
y
)
)
log
4
(
log
2
(
log
3
z
)
)
...
Đọc tiếp
Biết rằng log 2 ( log 3 ( log 4 x ) ) = log 3 ( log 4 ( log 2 y ) ) = log 4 ( log 2 ( log 3 z ) ) = 0 . Tính tổng x + y + z
A. 50
B. 58
C. 89
D. 111
Chọn C
Ta có:
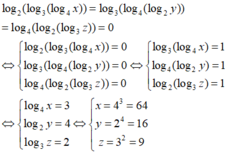
Từ đó x + y + z = 64 + 16 + 9 = 89
Đúng 0
Bình luận (0)
Nghiệm của phương trình log 4 { 2 log 3 [ 1 + log 2 ( 1 + 3 log 2 x ) ] } = 1/2 là
A. x = 1 B. x = 2
C. x = 3 D. x = 0
Tìm số nghiệm của phương trình log2(x)-log4(x-3)=2
ĐKXĐ: \(x>3\)
\(\log_2x-\dfrac{1}{2}log_2\left(x-3\right)=2\)
\(\Leftrightarrow2\log_2x-log_2\left(x-3\right)=4\)
\(\Leftrightarrow\log_2\dfrac{x^2}{x-3}=4\)
\(\Leftrightarrow\dfrac{x^2}{x-3}=16\)
\(\Leftrightarrow x^2-16x+48=0\Rightarrow\left[{}\begin{matrix}x=12\\x=4\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Giải bất phương trình log 4 ( x + 7 ) > log 2 ( x + 1 )
A. x> -1
B. x> 5
C. -1< x <2
D. x< 1
log2 x+log5 (x+8) =2 giải pt
Lời giải:
\(\log_2x+\log_5(x+8)=2\)
\(\Leftrightarrow \log_25.\log_5x+\log_5(x+8)=2\)
\(\Leftrightarrow \log_5(x^{\log_25})+\log_5(x+8)=2\)
\(\Leftrightarrow \log_5(x^{\log_25}(x+8))=2\)
\(\Leftrightarrow x^{\log_25}(x+8)=25\)
PT này mình nghĩ không giải theo kiểu thông thường. Shift-solve thôi ra $x=1,515$
Đúng 0
Bình luận (0)
Nghiệm của bất phương trình
log
4
(
x
+
7
)
log
2
(
x
+
1
)
là A. x -1 B. x 5 C. -1 x 2 D. x 1
Đọc tiếp
Nghiệm của bất phương trình log 4 ( x + 7 ) > log 2 ( x + 1 ) là
A. x > -1
B. x > 5
C. -1 < x < 2
D. x < 1
Bất phương trình
log
4
(
x
+
7
)
log
2
(
x
+
1
)
có tập nghiệm là A. (2;4) B. (-3;2) C. (-1;2) D. (5;
+
∞
)
Đọc tiếp
Bất phương trình log 4 ( x + 7 ) > log 2 ( x + 1 ) có tập nghiệm là
A. (2;4)
B. (-3;2)
C. (-1;2)
D. (5; + ∞ )
Bất phương trình log4 (x + 7) log2 (x + 1) có bao nhiêu nghiệm nguyên? A. 1 B. 2 C. 4 D. 3
Đọc tiếp
Bất phương trình log4 (x + 7) > log2 (x + 1) có bao nhiêu nghiệm nguyên?
A. 1
B. 2
C. 4
D. 3
Đáp án C
ĐK: x > –1
Khi đó PT
⇔ log 2 2 x + 7 > log 2 ( x + 1 )
⇔ 1 2 log 2 x + 7 > log 2 x + 1
⇔ log 2 x + 7 > log 2 x + 1 2
⇔ x + 7 > x + 1 2 ⇔ x 2 + x - 6 < 0
⇔ - 3 < x < 2
Kết hợp dk => -1<x<2 => x=0; x=1.
Đúng 0
Bình luận (0)
Bất phương trình
log
4
(
x
+
7
)
log
2
(
x
+
1
)
có bao nhiêu nghiệm nguyên? A. 1 B. 2 C. 4 D. 3
Đọc tiếp
Bất phương trình log 4 ( x + 7 ) > log 2 ( x + 1 ) có bao nhiêu nghiệm nguyên?
A. 1
B. 2
C. 4
D. 3