Cho tam giác ABC vuông tại A và có đường cao AH. Gọi I,K lần lượt là trung điểm của HC; AC và D là điểm đối xứng của A qua I
1/ Chứng minh: HD//AC và HC là phân giác của góc KHD
2/ Chứng minh AH+AC>2AI
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có đường cao AH, gọi I,K lần lượt là trung điểm của HC, AC. Chứng minh: a. HD//AC và HC là đường phân giác của góc KHD. b. AH+HC>2AI c. Tính AH, biết AB= 6cm, AC=8cm
Cho tam giác ABC vuông tại A. Đường cao AH. Lấy I là trung điểm của AC.
a) Chứng minh I là giao điểm của 3 đường trung trực tam giác AHC. Gọi K và D lần lượt là trung điểm của AH và HC. Chứng minh KD // AC.
b) Chứng minh BK vuông góc với AD.
a: ΔHAC vuông tại H
=>ΔHAC nội tiếp đường tròn đường kính AC
=>I là giao điểm của 3 đường trung trực của ΔAHC
Xét ΔHAC có HK/HA=HD/HC
nên KD//AC
b: DK//AC
AC vuông góc AB
=>DK vuông góc AB
Xét ΔBAD có
DK,AH là đường cao
DK cắt AH tại K
=>K là trực tâm
=>BK vuông góc AD
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A và có đường cao AH. Gọi I,K lần lượt là trung điểm của HC; AC và D là điểm đối xứng của A qua I
1/ Chứng minh: HD//AC và HC là phân giác của góc KHD
2/ Chứng minh AH+AC>2AI
Cho tam giác ABC vuông tại A đường cao AH BC=20cm và góc ACB=30 M là trung điểm BC (Gọi N, K lần lượt là trung điểm của AC và HC)
C/m KN là tiếp tuyến của (I)đường kính AM
Xem chi tiết
Cho tam giác ABC vuông tại A đường cao AH . Gọi I , K lần lượt là hình chiếu của AB , AC a) Tứ giác AHBC là tứ giác gì . Vì sao ? b)Chứng minh : IK = AH c) Gọi M là trung điểm của HC , O là giao điểm của AH và IK . Chứng minh BO vuông góc AM
b: Xét tứ giác AIHK có
\(\widehat{KAI}=\widehat{AIH}=\widehat{AKH}=90^0\)
Do đó: AIHK là hình chữ nhật
Suy ra: IK=AH
Đúng 0
Bình luận (0)
BT: Cho tam giác ABC vuông tại A, đường cao AH, gọi D,E lần lượt là chân các đường vuông góc kẻ từ H đến AB và AC a) Chứng minh AH=DE b) Gọi I là trung điểm của HB, K là trung điểm của HC. Chứng minh DI song song với EK
Xem chi tiết
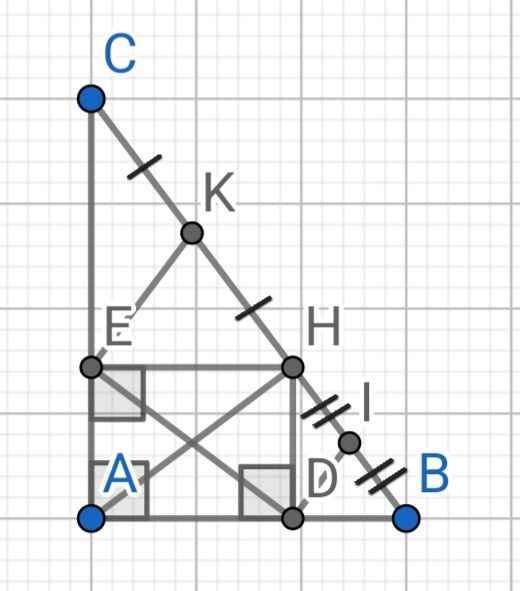a) Tứ giác ADHE có:
∠AEH = ∠ADH = ∠HAE = 90⁰ (gt)
⇒ ADHE là hình chữ nhật
⇒ AH = DE
b) BHD vuông tại D
I là trung điểm của HB (gt)
⇒ ID = IH = BH : 2
⇒ ∆IDH cân tại I
⇒ ∠IDH = ∠IHD
⇒ ∠HID = 180⁰ - (∠IDH + ∠IHD)
= 180⁰ - 2∠IHD (1)
∆CEH vuông tại E
K là trung điểm HC (gt)
⇒ KE = KC = HC : 2
⇒ ∆KEC cân tại K
⇒ ∠KEC = ∠KCE
⇒ ∠CKE = 180⁰ - (∠KEC + ∠KCE)
= 180⁰ - 2∠KEC (2)
Do HD ⊥ AB (gt)
AC ⊥ AB (gt)
⇒ HD // AC
⇒ ∠IHD = ∠KCE (đồng vị)
⇒ 2∠IHD = 2∠KCE (3)
Từ (1), (2) và (3) ⇒ ∠CKE = ∠HID
Mà ∠CKE và ∠HID là hai góc đồng vị
⇒ DI // KE
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A có AH là đường cao . Gọi d và e lần lượt là hình chiếu của H xuống AB và AC.Gọi I là trung điểm của HB, K là trung điểm HC. Chứng minnh: a) DI song song EK
b) Gọi F là trung điểm IK. Chứng minh tam giác DEF cân
cho tam giác ABC vuông tại A có đường cao AH, gọi EF lần lượt là hình chiếu của H lên AB và AC a) chứng minh AH=EF b) gọi M là trung điểm của BC chứng minh AM vuông góc với EF c) gọi I,J lần lượt là trung điểm của HB, HC chứng ming tứ giác IEFJ là hình thang vuông
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AH=FE
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a có ah là đg cao gọi P và Q lần lượt là hình chiếu của H xuống AB,Ac gọi i là trung điểm của HB. k là trung điểm của HC AH cắt PQ ở O
a; Tg APHQ là hình gì b;Tam giác KQH là tam giác gì
a/
\(AQ\perp AB;PH\perp AB\) => AQ//PH
\(AP\perp AC;QH\perp AC\) => AP//QH
=> APHQ là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Ta có \(\widehat{A}=90^o\)
=> APHQ là hình chữ nhật (Hình bình hành có 1 góc vuông là HCN)
b/
Xét tg vuông QHC có
KH=KC (gt)
\(\Rightarrow QK=\dfrac{AC}{2}\) (Trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
Mà \(KH=KC=\dfrac{HC}{2}\)
=> QK=KH => tg KQH cân tại K
Đúng 0
Bình luận (0)