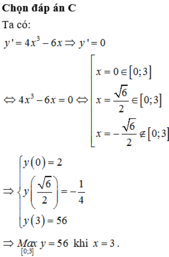tim GTNN của x4 +3x2-4 bằng

Những câu hỏi liên quan
Tìm GTNN của biểu thức:
M= (x4 + 3x3 + 3x2 - 3x - 4):( x2 - 1)
Giá trị lớn nhất của hàm số y = x 4 - 3 x 2 + 2 trên đoạn [0;3] bằng
A. 57
B. 55
C. 56
D. 80
Giá trị lớn nhất của hàm số y = x 4 - 3 x 2 + 2 trên đoạn 0 ; 3 bằng
A. 57
B. 55
C. 56
D. 58
Cho x,y la cac so duong thoa man : x+y≤1. Tim GTNN cua:
P=(x4+y4+1)(1/x4+1/y4+1)
Cho x,y la cac so duong thoa man : x+y≤1. Tim GTNN cua:
P=(x4+y4+1)(1/x4+1/y4+1)
Can gap mn oi!!!
\(P=\left(x^4+y^4+\dfrac{1}{256}+\dfrac{255}{256}\right)\left(\dfrac{1}{x^4}+\dfrac{1}{y^4}+1\right)\)
\(P=\left(x^4+y^4+\dfrac{1}{256}\right)\left(\dfrac{1}{x^4}+\dfrac{1}{y^4}+1\right)+\dfrac{255}{256}\left(\dfrac{1}{x^4}+\dfrac{1}{y^4}+1\right)\)
\(P\ge\left(\dfrac{x^2}{x^2}+\dfrac{y^2}{y^2}+\dfrac{1}{16}\right)^2+\dfrac{255}{256}\left(\dfrac{1}{2}\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)^2+1\right)\)
\(P\ge\left(\dfrac{33}{16}\right)^2+\dfrac{255}{256}\left(\dfrac{1}{2}\left(\dfrac{1}{2}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\right)^2+1\right)\)
\(P\ge\left(\dfrac{33}{16}\right)^2+\dfrac{255}{256}\left(\dfrac{1}{8}\left(\dfrac{4}{x+y}\right)^4+1\right)\ge\left(\dfrac{33}{16}\right)^2+\dfrac{255}{256}\left(\dfrac{4^4}{8}+1\right)=\dfrac{297}{8}\)
\(P_{min}=\dfrac{297}{8}\) khi \(x=y=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Tính
l
i
m
x
→
∞
x
4
-
3
x
2
+
4
A. 4. B. 1. C.
-
∞
. D.
+
∞
.
Đọc tiếp
Tính l i m x → ∞ x 4 - 3 x 2 + 4
A. 4.
B. 1.
C. - ∞ .
D. + ∞ .
Tính lim x → ∞ ( x 4 - 3 x 2 + 4 )
A.4
B.1
C. - ∞
D. + ∞
Đồ thị sau đây là của hàm số y
x
4
-
3
x
2
-
3
. Với giá trị nào của m thì phương trình
x
4
-
3
x
2
-
3
-
m
có 3 nghiệm phân biệt A. m -4 B. m -3 C. 0 D. m -5
Đọc tiếp
Đồ thị sau đây là của hàm số y = x 4 - 3 x 2 - 3 . Với giá trị nào của m thì phương trình x 4 - 3 x 2 - 3 - m có 3 nghiệm phân biệt
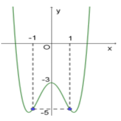
A. m = -4
B. m = -3
C. 0
D. m = -5
Đồ thị sau đây của hàm số y
x
4
-
3
x
2
-
3
. Với giá trị nào của m thì phương trình
x
4
-
3
x
2
+
m
0
có ba nghiệm phân biệt? A. m -4 B. m 0. C. m -3. D. m 4.
Đọc tiếp
Đồ thị sau đây của hàm số y = x 4 - 3 x 2 - 3 . Với giá trị nào của m thì phương trình x 4 - 3 x 2 + m = 0 có ba nghiệm phân biệt?
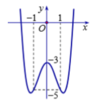
A. m = -4
B. m = 0.
C. m = -3.
D. m = 4.
Chọn B.
Ta có:
x
4
-
3
x
2
+
m
=
0
![]()
Dựa vào đồ thị ta có phương trình có 3 nghiệm phân biệt khi -m-3 = -3 => m = 0
Đúng 0
Bình luận (0)
Đồ thị sau đây của hàm số
y
x
4
-
3
x
2
-
3
.
Với giá trị nào của m thì phương trình
x
4
-
3
x
2...
Đọc tiếp
Đồ thị sau đây của hàm số y = x 4 - 3 x 2 - 3 . Với giá trị nào của m thì phương trình x 4 - 3 x 2 + m = 0 có ba nghiệm phân biệt?
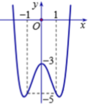
A.m=-4
B.m=0
C.m=-3
D.m=4
Chọn B.
Ta có:
x 4 - 3 x 2 + m = 0 ⇔ x 4 - 3 x 2 = - m ⇔ x 4 - 3 x 2 - 3 = - m - 3 .
Dựa vào đồ thị ta có phương trình có 3 nghiệm phân biệt khi
- m - 3 = - 3 ⇔ m = 0 .
Đúng 0
Bình luận (0)