Cho các điểm biểu diễn các cặp giá trị tương ứng là: O(0;0); A(1;2); B(2;4); C(3;6); D(4;8)
Chứng minh rằng O;A;B;C;D thẳng hàng
Help me (Không cần vẽ hình cx đc)
Những câu hỏi liên quan
Hàm số đc cho trong bảng sau: x -1 0 1 2 3 y -3 -1 1 3 5a) Viết các cặp giá trị (x;y) tương ứng của hàm số trên;b) Vẽ 1 hệ trục tọa độ Oxy và xác định các điểm biểu diễn các cặp giá trị của x và y tương ứng ở câu a.
Đọc tiếp
Hàm số đc cho trong bảng sau:
| x | -1 | 0 | 1 | 2 | 3 |
| y | -3 | -1 | 1 | 3 | 5 |
a) Viết các cặp giá trị (x;y) tương ứng của hàm số trên;
b) Vẽ 1 hệ trục tọa độ Oxy và xác định các điểm biểu diễn các cặp giá trị của x và y tương ứng ở câu a.
9 tháng 12 2021 lúc 20:52
Hàm số y được cho trong bảng sau:x01234y02468a) Viết tất cả các cặp giá trị tương ứng (x; y) của hàm số trên.b) Vẽ một hệ trục toạ độ Oxy và xác định các điểm biểu diễn các cặp giá trị tương ứng của x và y ở câu a.
Đọc tiếp
Hàm số y được cho trong bảng sau:
| x | 0 | 1 | 2 | 3 | 4 |
| y | 0 | 2 | 4 | 6 | 8 |
a) Viết tất cả các cặp giá trị tương ứng (x; y) của hàm số trên.
b) Vẽ một hệ trục toạ độ Oxy và xác định các điểm biểu diễn các cặp giá trị tương ứng của x và y ở câu a.
Cho các điểm biểu diễn các cặp giá trị tương ứng là: O(0;0); A(1;2); B(2;4); C(3;6); D(4;8)
Chứng minh rằng O;A;B;C;D thẳng hàng
Help me (Không cần vẽ hình cx đc)
nay ban k có hàm số làm sao chứng minh dc
Đúng 0
Bình luận (0)
Cho hàm số y = f(x) = 2x - 1
a) Tính: f(1); f(-1); f(0); f(2)
b) Lập bảng các giá trị tương ứng của x và y
c) Qua bảng hãy viết các cặp giá trị tương ứng của x và y (và đặt tên là điểm A; B; C; D)
d) Hãy biểu diễn các điểm đó trên mặt phẳng tọa độ Oxy
Hàm số y được cho bảng sau:
x
0
1
2
3
4
y
0
2
4
6
8
Vẽ một hệ trục tọa độ Oxy và xác định các điểm biểu diễn các cặp giá trị tương ứng của x và y ở câu a
Đọc tiếp
Hàm số y được cho bảng sau:
| x | 0 | 1 | 2 | 3 | 4 |
| y | 0 | 2 | 4 | 6 | 8 |
Vẽ một hệ trục tọa độ Oxy và xác định các điểm biểu diễn các cặp giá trị tương ứng của x và y ở câu a
Trên hình vẽ 0, A, B, C, D là vị trí của các điểm biểu diễn các cặp giá trị tương ứng của x và y trong câu a.
Đúng 0
Bình luận (0)
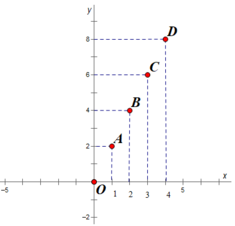
Cho \(y\) làm hàm số của biến số \(x\). Giá trị tương ứng của \(x;y\) được cho trong bảng sau:
a) Vẽ hệ trục tọa độ \(Oxy\) và xác định các điểm biểu diễn các cặp giá trị \(\left( {x;y} \right)\) tương ứng có trong bảng trên.
b) Em có nhận xét gì về điểm vừa xác định trong câu a?
a) Đồ thị hàm số là tập hợp các điểm có tọa độ \(\left( { - 2; - 6} \right);\left( { - 1; - 3} \right);\left( {0;0} \right);\left( {1;3} \right);\left( {2;6} \right)\) được vẽ trên mặt phẳng tọa độ như hình dưới đây
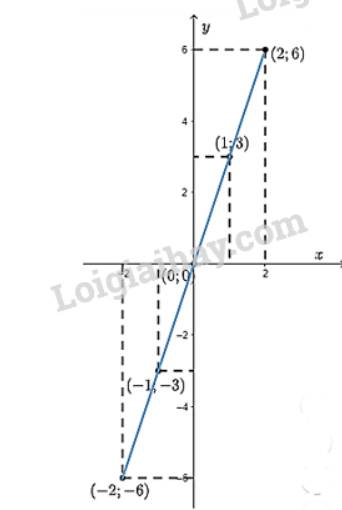
b) Các điểm vừa xác định được ở câu a đều nằm trên một đường thẳng.
Đúng 0
Bình luận (1)
Hàm số y được cho trong bảng sau :x01234y02468a) Viết tất cả các cặp giá trị tương ứng (x;y) của hàm số trên.b)Vẽ một hệ trục tọa độ Oxy và xác định các điểm biểu diễn các cặp giá trị tương ứng của x và y ở câu a.
Đọc tiếp
Hàm số y được cho trong bảng sau :
| x | 0 | 1 | 2 | 3 | 4 |
| y | 0 | 2 | 4 | 6 | 8 |
a) Viết tất cả các cặp giá trị tương ứng (x;y) của hàm số trên.
b)Vẽ một hệ trục tọa độ Oxy và xác định các điểm biểu diễn các cặp giá trị tương ứng của x và y ở câu a.
a) 0(0;0),A(1;2),B(2;4),C(3;6),D(4;8)
b) vẽ khó lắm :)
Đúng 0
Bình luận (0)
Cho hàm số y = f(x) = 2x - 1
a) Tính: f(1); f(-1); f(0); f(2)
b) Lập bảng các giá trị tương ứng của x và y
c) Qua bảng hãy viết các cặp giá trị tương ứng của x và y (và đặt tên điểm A; B; C; D)
a) Thay x=1 vào hàm số y=2x-1, ta được:
\(y=2\cdot1-1=2-1=2\)
Thay x=-1 vào hàm số y=2x-1, ta được:
\(y=2\cdot\left(-1\right)-1=-2-1=-3\)
Thay x=0 vào hàm số y=2x-1, ta được:
\(y=2\cdot0-1=-1\)
Thay x=2 vào hàm số y=2x-1, ta được:
\(y=2\cdot2-1=4-1=3\)
Vậy: F(1)=2; F(-1)=-3; F(0)=-1; F(2)=3
b)
x 1 -1 0 2 y=2x-1 2 -3 -1 3
Đúng 1
Bình luận (0)
SGK Cánh Diều
13 tháng 8 2023 lúc 21:20
Cho hàm số lôgarit y {log _{frac{1}{2}}}xa) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:b, Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a.Bằng cách làm tương tự, lấy nhiều điểm left( {x;{{log }_{frac{1}{2}}}x} right) với x in (0; + infty ) và nối lại ta được đồ thị hàm số y {log _{frac{1}{2}}}x như hình bên.c, Cho biết tọa độ giao điểm của đồ thị hàm số y {log _{frac{1}{2}}}x với trục hoành và vị trí của đồ thị hàm số đó với trục tung.d,...
Đọc tiếp
Cho hàm số lôgarit \(y = {\log _{\frac{1}{2}}}x\)
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
b, Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a.
Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;{{\log }_{\frac{1}{2}}}x} \right)\) với \(x \in (0; + \infty )\) và nối lại ta được đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\) như hình bên.
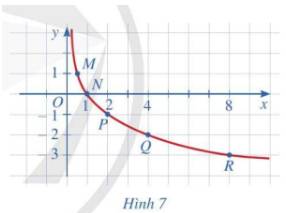
c, Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\) với trục hoành và vị trí của đồ thị hàm số đó với trục tung.
d, Quan sát đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\), nêu nhận xét về:
\(\mathop {\lim }\limits_{x \to {0^ + }} ({\log _{\frac{1}{2}}}x)\,;\mathop {\,\,\mathop {\lim }\limits_{x \to + \infty } ({{\log }_{\frac{1}{2}}}x)}\limits_{} \)Sự biến thiên của hàm số \(y = {\log _{\frac{1}{2}}}x\) và lập bảng biến thiên của hàm số đó.
a:
| x | 0,5 | 1 | 2 | 4 | 8 |
| \(y\) | -1 | 0 | 1 | 2 | 3 |
b:
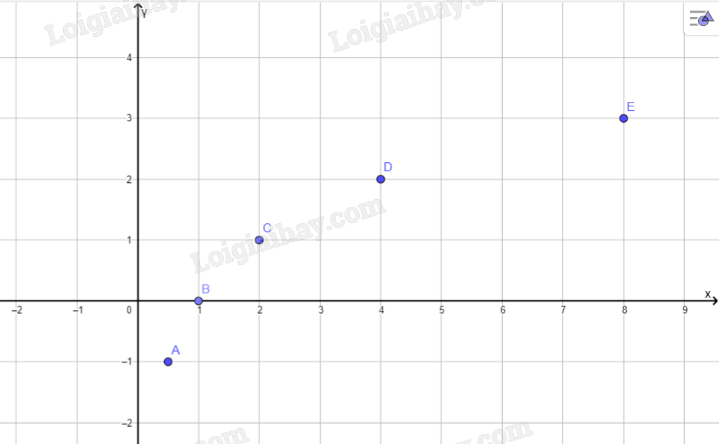
c: Tọa độ giao điểm của hàm số với trục hoành là B(2;0)
Đồ thị hàm số này ko cắt trục tung
d:
\(\lim\limits_{x\rightarrow0^+}log_2x=0\)
\(\lim\limits_{x\rightarrow+\infty}\left(log_2x\right)=+\infty\)
=>Hàm số này đồng biến trên TXĐ của nó là D=[0;+vô cực)
Đúng 0
Bình luận (0)