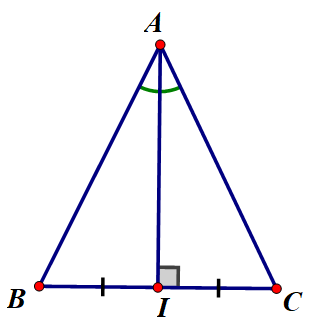
Chứng minh : trong một tam giác cân, đường phân giác xuất phát từ đỉnh đồng thời là đường trung tuyến ứng với cạnh đáy.

Những câu hỏi liên quan
Chứng minh rằng trong một tam giác cân, đường trung trực ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến và đường cao cùng xuất phát từ đỉnh đối diện với cạnh đó
bạn tham khảo link này nha:https://hoc24.vn/hoi-dap/tim-kiem?id=137279&q=Ch%E1%BB%A9ng%20minh%20%3A%20trong%20m%E1%BB%99t%20tam%20gi%C3%A1c%20c%C3%A2n%2C%20%C4%91%C6%B0%E1%BB%9Dng%20ph%C3%A2n%20gi%C3%A1c%20xu%E1%BA%A5t%20ph%C3%A1t%20t%E1%BB%AB%20%C4%91%E1%BB%89nh%20%C4%91%E1%BB%93ng%20th%E1%BB%9Di%20l%C3%A0%20%C4%91%C6%B0%E1%BB%9Dng%20trung%20tuy%E1%BA%BFn%20%E1%BB%A9ng%20v%E1%BB%9Bi%20c%E1%BA%A1nh%20%C4%91%C3%A1y.
Đúng 1
Bình luận (0)
chứng minh rằng trong một tam giác cân đường cao suất phát từ định đối diện với cạnh đáy đồng thời là đường phân giác cùng xuất phát từ đỉnh này
chứng minh rằng trong một tam giác cân, đường cao xuất phát từ đỉnh đối diện với đáy đồng thời là đường phân giác cùng xuất phát từ đỉnh này
chứng minh rằng trong tam giác cân đường trung tuyến xuất phát từ đỉnh đồng thời là tia phân giác
Giả sử \(\Delta ABC\)cân tại A có AM là trung tuyến .
Xét \(\Delta AMB\)và \(\Delta AMC\)có :
AB = AC ( gt )
AM ( cạnh chung )
BM = CM ( gt )
Suy ra : \(\Delta AMB\)= \(\Delta AMC\)( c.c.c )
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\)
Từ đó suy ra ; AM là tia phân giác của \(\Delta ABC\)
Đúng 0
Bình luận (0)
Nhận xét Trong một tam giác, nếu hai trong bốn loại đường ( đường trung tuyến, đường phân giác, đường cao cùng xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của cạnh này ) trùng nhau thì tam giác đó là một tam giác cân.Từ nhận xét trên hãy chứng minh: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân ai nhank mk tick cho help me tói 9h tối nay phải có nha mk gấp lắm
Đọc tiếp
Nhận xét
Trong một tam giác, nếu hai trong bốn loại đường ( đường trung tuyến, đường phân giác, đường cao cùng xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của cạnh này ) trùng nhau thì tam giác đó là một tam giác cân.
Từ nhận xét trên hãy chứng minh: "Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân "
ai nhank mk tick cho help me tói 9h tối nay phải có nha mk gấp lắm
Xét tam giác ABC có AI là đường trung trực vừa là đường phân giác
vì AI là đường trung trực nên AI vuông góc với BC và I là trung điểm cuả BC
xét 2 tam giác vuông ABI và tam giác vuông ACI có;
IA chung
góc BAI=gócCAI (do AI là phân giác)
do đó tam giác BAI =tam giác CAI
suy ra AB=AC (2 cạnh tương ứng)
suy ra tam giác ABC cân tại A (định nghĩa tam giác cân)
Đúng 0
Bình luận (0)
Trong tam giác cân đường phân giác xuất phát từ đỉnh với cạnh đáy đối diện có đồng thời là đường trung trực hay không?
bài 1: chứng minh 1 tam có 2 đường trung tuyến bằng nhau thì tam giác đó cân
bài 2: chứng minh trong tam giác cân 2 đường cao ứng với 2 cạnh bên và ngược lại có 2 đường cao bằng nhau là tam giác cân
bài 3:chứng minh 2 đường phân giác xuất phát từ 2 đỉnh ở đấy của tam giác cân thì bằng nhau và ngược lại 1 tam giác có 2 đg phân giác bằng nhau thì là tam giác ân
câu 1 :đúng hay sai
a)hai tam giác bằng nhau thì hai đường trung tuyến tương ứng bằng nhau
b)hai tam giác bằng nhau thì hai đường phân giác tương ứng bằng nhau
c)hai tam giác bằng nhau thì hai đường cao tương ứng bằng nhau
d)trong tam giác cân đường trung tuyến xuất phát từ đỉnh đồng thời là đường phân giác , đường cao, đường trung trực
a) Chứng minh trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b) Chứng minh rằng trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.
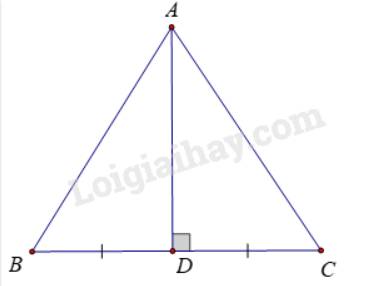
a) Kẻ đường trung trực của đoạn thẳng BC, cắt BC tại D
Ta có: Tam giác ABC cân nên AB = AC
\( \Rightarrow A\)thuộc đường trung trực của cạnh BC (t/c)
\( \Rightarrow AD\)là đường trung trực của BC.
Xét \(\Delta ABD\)và \(\Delta ACD\)có:
AB = AC (gt)
BD = CD (gt)
AD: cạnh chung
\( \Rightarrow \Delta ABD = \Delta ACD\left( {c - c - c} \right)\)
\( \Rightarrow \widehat {BAD} = \widehat {CAD}\)
\( \Rightarrow \)AD là tia phân giác góc BAC.
Vậy tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b)
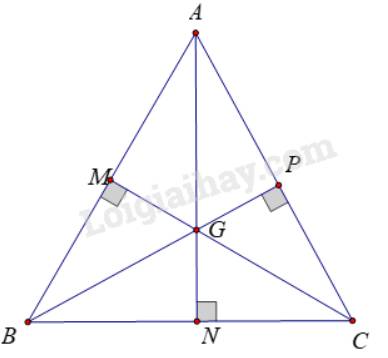
Ta có: Điểm cách đều ba đỉnh của tam giác là giao điểm ba đường trung trực của tam giác đó.
Tam giác ABC đều nên AB = BC = CA
Tam giác ABC cân tại A có AN là đường trung tuyến
\( \Rightarrow \) AN là đường phân giác xuất phát từ đỉnh A (cm ở ý a)
Tương tự: BP, CM lần lượt là đường phân giác xuất phát từ B và C của tam giác ABC
Mà AN cắt BP tại G
\( \Rightarrow G\) là giao điểm ba đường phân giác của tam giác ABC
\( \Rightarrow G\) cách đều ba cạnh của tam giác ABC (Tính chất
Đúng 0
Bình luận (0)