cho hình chữ nhật ABCD và một điểm M trong hình chữ nhật đó. Chứng minh rằng : MA^2+MC^2=MB^2+MD^2
Cho hình chữ nhật ABCD. Một điểm M nằm trong hình chữ nhật và điểm N nằm ngoài hình chữ nhật đó sao cho AN = CM, DN = BM. Chứng minh:
Diện tích AMDN = \(\frac{1}{2}\)diện tích ABCD
Cho hình chữ nhật ABCD, M là một điểm bất kì nằm trong hình chữ nhật đó. Chứng minh MA + MC + MB + MD < AB+AD+AC.
Cho hình 125 trong đó ABCD là hình chữ nhật, E là một điểm bất kì nằm trên đường chéo AC, FG // AD và HK // AB. Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích.
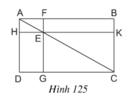
Ta có: SEHDG = SADC – SAHE – SEGC.
SEFBK = SABC – SAFE – SEKC.
Để chứng minh SEHDG = SEFBK,
ta đi chứng minh SADC = SABC; SAHE = SAFE ; SEGC = SEKC.
+ Chứng minh SADC = SABC.
SADC = AD.DC/2;
SABC = AB.BC/2.
ABCD là hình chữ nhật ⇒ AB = CD, AD = BC
⇒ SADC = SABC.
+ Chứng minh SAHE = SAFE (1)
Ta có: EH // AF và EF // AH
⇒ AHEF là hình bình hành
Mà Â = 90º
⇒ AHEF là hình chữ nhật
⇒ SAHE = SAFE (2)
+ Chứng minh SEGC = SEKC
EK // GC, EG // KC
⇒ EGCK là hình bình hành
Mà D̂ = 90º
⇒ EGCK là hình chữ nhật
⇒ SEGC = SEKC (3).
Từ (1); (2); (3) suy ra đpcm.
Cho hình 125, trong đó ABCD là hình chữ nhật, E là một điểm bất kì nằm trên đường chéo AC, FG // AD và HK // AB. Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích.
Cho hình chữ nhật ABCD. Qua một điểm M tùy ý nằm ở bên trong hình chữ nhật đó, kẻ các đường thẳng song song với các hình chữ nhật, chia hình chữ nhật thành 4 hình chữ nhật nhỏ. CMR ít nhất một trong hai hình chữ nhật nhỏ chứa đỉnh A hoặc đỉnh C có diện tích không vượt quá 1/4 diện tích hình chữ nhật ABCD
Cho hình chữ nhật ABCD. Lần lượt quay hình chữ nhật đó một vòng quanh cạnh BC và một vòng quanh cạnh CD, ta được hai hình trụ có diện tích toàn phần bằng nhau. Chứng minh tứ giác ABCD là hình vuông
Khi quay hình chữ nhật quanh cạnh BC:
Stp trụ = 2π.AB.AD + 2π. A B 2 = S 1
Khi quay cạnh CD: Stp trụ = 2π.AB.AD + 2π. B C 2 = S 2
Mặt khác: S 1 = S 2 <=> 2π.AB.AD + 2π. A B 2 = 2π.AB.AD + 2π. B C 2
<=> AB = BC => ABCD là hình vuông
a] Để chứng minh AF // BD, ta cần chứng minh tỉ số đồng dạng giữa các cặp cạnh tương ứng của hai tam giác ACF và BDE. Ta có:
AC/BD = AD/BE (vì AF // BD) AC/AD = BE/BD (vì AM // BD và BN // BD)
Từ hai tỉ số trên, ta có:
AC/AD = BE/BD
Vậy, ta đã chứng minh được AF // BD.
b] Để chứng minh E là trung điểm CF, ta cần chứng minh CE = EF và CF // AB. Ta có:
CE = AM (vì CE // AM và AC // BD) EF = BN (vì EF // BN và AC // BD)
Vậy, ta đã chứng minh được E là trung điểm CF.
Cho hình chữ nhật ABCD , M là điểm bất kì trong hình chữ nhật ABCD . Chứng minh rằng MA^2 + MC^2 = MB^2 + MD^2
vẽ hình giùm mình với nha giải dc sẽ like
Cho hình chữ nhật ABCD , M là điểm bất kì trong hình chữ nhật ABCD. Chứng minh rằng MA^2 + MC^2 = MB^2 + MD^2
Vẽ hình giúp mình với nha ai giải dc mình like cho