Cho tam giác ABC có E thuộc cạnh AB, D thuộc cạnh AC và M thuộc cạnh BC sao cho EM // AC; MD // AB. Gọi I là trung điểm của ED. Khi đó số đo của AIM là

Những câu hỏi liên quan
Cho tam giác ABC có E thuộc cạnh AB, D thuộc cạnh AC và M thuộc cạnh BC sao cho EM // AC; MD // AB. Gọi I là trung điểm của ED. Khi đó số đo của AIM là
Cho tam giác ABC có E thuộc cạnh AB, D thuộc cạnh AC và M thuộc cạnh BC sao cho EM // AC; MD // AB. Gọi I là trung điểm của ED. Khi đó số đo của AIM là
Vì EM//AC và MD//AB => AEMD là hình bình hành( dấu hiệu nhận biết) mà I là trung điểm ED => I cũng là trung điểm AM (tính chất của hình bình hành) => I,A,M thẳng hàng hay góc AIM =180 độ :)
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC có BC=12cm, đường cao AH=6cm. Hình vuông DEMN có D thuộc cạnh AB, E thuộc cạnh AC, M và N thuộc cạnh BC. Tính Sdemn
Bài 1: Tam giác ABC và tam giác MNP đồng dạng, Biết
BC= 10; AC= 12. Tính số đo các góc C, M, N, P và độ dài cạnh NP.
Bài 2: Cho tam giác ABC có AB = 8cm, AC = 16cm. Điểm D thuộc cạnh AB sao cho BD
= 2cm. Điểm E thuộc cạnh AC sao cho CE = 13cm. Chứng minh rằng:
a) Δ AED ω ΔΑBC
b) ABE = ACD
Bài 2:
a: AE=AC-CE=16-13=3(cm)
AD=AB-BD=8-2=6(cm)
Xét ΔAED và ΔABC có
AE/AB=AD/AC
\(\widehat{A}\) chung
Do đó: ΔAED∼ΔABC
b: Ta có: ΔAED∼ΔABC
nên AE/AB=AD/AC
hay AB/AC=AE/AD
Xét ΔABE và ΔACD có
AB/AC=AE/AD
\(\widehat{BAE}\) chung
Do đó: ΔABE∼ΔACD
Suy ra: \(\widehat{ABE}=\widehat{ACD}\)
Đúng 3
Bình luận (0)
cho tam giác ABC, E thuộc cạnh BC, kẻ ED song song với cạnh AB ,EM song song với AC (D thuộc AC; M thuộc AB). Chứng minh rằng 2 đoạn thẳng AE và MD cắt nhau tại trung điểm của mỗi đường
Xét tứ giác AMED có
AM//ED
EM//AD
Do đó: AMED là hình bình hành
Suy ra: AE và MD cắt nhau tại trung điểm của mỗi đường
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB<AC), lấy D thuộc cạnh AB,E thuộc cạnh AC sao cho BD = CE. Gọi M,N theo thứ tự là trung điểm của BC và DE
a) CMR : MN // với tia phân giác của góc A
cho tam giác ABC có AB = 9cm; điểm D thuộc cạnh AB sao cho AD = 6cm. Kẻ DE//BC (E thuộc AC) , Kẻ EF//CD ( F thuộc AB ). Độ dài cạnh AF là ... cm :))
Cho tam giác ABC. Lấy D thuộc cạnh AB, E thuộc cạnh AC sao cho DE // BC. Gọi M là trung điểm của BC, AM cắt DE tại N . Chứng minh ND =NE .
Xét ΔAMB có ND//MB
nên ND/MB=AN/AM
Xét ΔAMC có NE//MC
nên NE/MC=AN/AM
=>ND/MB=NE/MC
=>ND=NE
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB 8cm, AC 16cm. Điểm D thuộc cạnh AB sao cho BD 2cm. Điểm E thuộc cạnh AC sao cho CE 13cm. Chọn câu sai. A.
A
B
E
^
A
C
D
^
B. AE.CD AD. BC C.
A
E
.
B
C
A
B...
Đọc tiếp
Cho tam giác ABC có AB = 8cm, AC = 16cm. Điểm D thuộc cạnh AB sao cho BD = 2cm. Điểm E thuộc cạnh AC sao cho CE = 13cm. Chọn câu sai.
A. A B E ^ = A C D ^
B. AE.CD = AD. BC
C. A E . B C = A B . E D
D. AE.AC = AD.AB
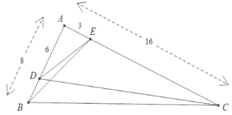
+ Xét ΔABE và ΔACD có A chung và A E A D = A B A C ( = 1 2 ) nên
ΔABE ~ ΔACD (c - g - c) suy ra góc A B E ^ = A C D ^ (hai góc tương ứng) và => AE.CD = AD.BE
+ ΔAED ~ ΔABC (cmt) nên A E A B = A D A C ⇔ AE.AC = AB.AD
Nên A, C, D đúng, B sai.
Đáp án: B
Đúng 0
Bình luận (0)















